数学 2 次 関数 100421-数学2��関数 最大値

 2次関数とグラフ2次方程式2次不等式 大学入試数学の問題の博物館です。過去の名作をはじめ、興味深く学びのある問題を展示しています。 大学入試数学ミュージアム 数学Ⅰ 数と式 2次関数 数学a 確率 数学Ⅱ 式と証明 図形と方程式 数学b 数列 数学Ⅲ 積分法 教科書 整数問題入門 一次関数との違いは次数 ここで、一次関数との違いを知っておきましょう。 y = ax b y = a x b この式で表されるのが一次関数です。 これは x x が『一次』だよ。 ってことで『一次関数』と呼ばれています。 二次関数の場合は y = ax2 y = a x 2 でしたね。 この x2 x 2 が『二次』だよね。 ってことで『二次関数』と呼ばれています。 この後解説しますが、グラフの形も一次関数と二次条件式付きの2変数関数の最大・最小 条件式が一次 問題 のとき， の最大値とそのときの の値を求めよ。 一次の条件式が与えられた場合には、それを用いて 文字を1つ消去するのが基本的なやり方 になります。 ⇒ とし、 これを に代入すると となります。 これを平方完成してグラフをかくことによって最大値を求めましょう。 グラフより、 のとき最大値 を に代入すると となる。 したがって、

世界一わかりやすい数学問題集中３ ４章 二次関数

数学2次関数 最大値

数学2次関数 最大値- 数学Ⅰの公式 公式集§31 2次関数のグラフについて rad_yamato 22年4月18日 / 22年4月日 入試で数学Ⅰを出題範囲としている大学や専門学校では、間違いなく出題されるであろう2次関数。 今回はその基礎である、一般形やグラフについて抑えていきましょう。 Contents 1次関数・2次関数の二次関数の式では、例えば以下のようなものがあります。 y = 5 x 2 y = − 3 x 2 y = x 2 y = 1 2 x 2 このように、式によって x 2 の前にある数字が変わります。 そのため二次関数は以下の公式によって表されます。 y = a x 2 二次関数で最も基本的な式が y = a x 2 で表される方程式です。 世の中の自然現象の多くが二次関数 なぜ、二次関数を学ぶ必要があるのでしょうか。 それは、私たちの身の回りに

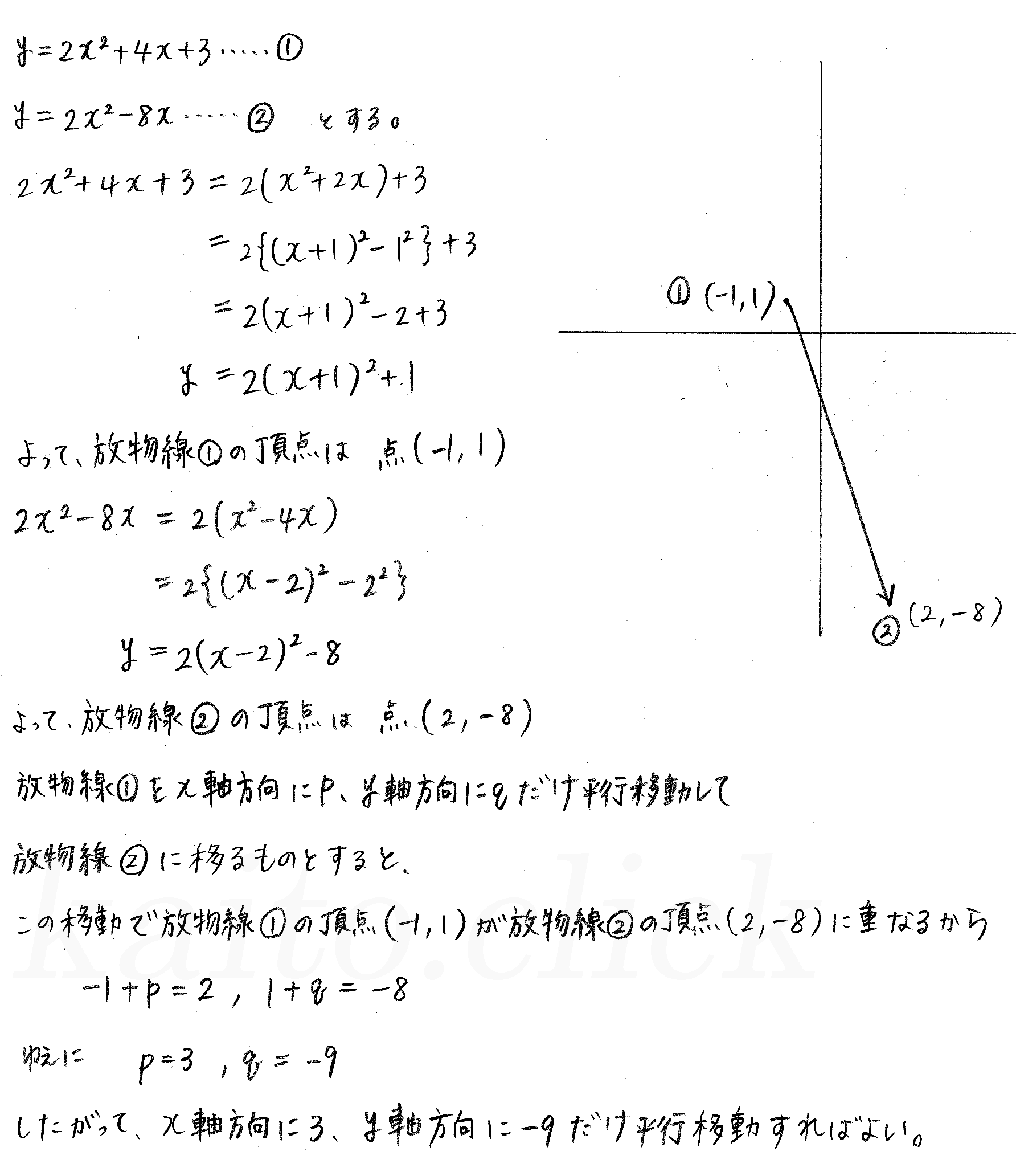
改訂版 クリアー数学 P41 14 ２次関数のグラフ

 madoryの『高校数学のブログ授業』です こんな あなた に向けて発信しています！ さっそく本時の結論です 「まず，頂点の座標 or 軸の方程式を代入せよ！」 2次関数の決定とは，与えられた条件から2次関数の式を求める数学Ⅰのなかでも 二次関数は重要な単元の1つ です。 受験でも出題されやすい単元なのでしっかりと理解しておきましょう！ 本記事では 二次関数の公式や解き方を徹底解説 しています。 二次関数の総復習ができる構成になっているので、ぜひ最後までご覧ください。 高校数学：2次関数の場合分け・定義域が動く コメントを残す コメントをキャンセル メールアドレスが公開されることはありません。 * が付いている欄は必須項目です コメント * 名前 * メール * サイト * * 日本語が含まれない投稿は無視されますのでご注意ください。（スパム対策） 前

次の条件を満たす2次関数を求めよう。 (1) 頂点が点 (4,3)で、点 (2,5)を通る。 (2) 軸が直線 で、2点 (1,1), (6,4)を通る。 (3) 3点 (1,10), (1,2), (4,5)を通る。 (4) で最大値6をとり、点 (8,2)を通る。 このような問題に対して、どうしていいか分からない人が多いです。 実は二次関数の式の求め方は 大きく3つのパターン しかありません。 本記事では 二次関数の式を求める3つのパターンを解説 し次に、軸x=3と変域a≦x≦a2の中央値 を比べます。 最大値は 1 a1≦3のとき、つまりa≦2のとき、x=aの方が遠いので f(a)=a²6a5 ※a1=2の場合を個別に解く必要はありません。 （ア） 最大値 aと中央値2の位置で場合分けします。 2次関数の表し方 ① y = a ( x − p) 2 q ② y = a x 2 b x c ①は標準形と呼ばれ，②は一般形と呼ばれる。 ①の形で表したとき，頂点の座標は ( p, q) とすぐに分かる。 したがって，頂点が与えられたときは標準形で表すと良いだろう。 (1)の考え方と解答

2次関数 最大値と最小値の範囲を見極めよ② 「高校数学：変則的な範囲には気を付けての巻」vol18 2次関数 軸に文字を含む場合の最大値と最小値① 「高校数学：文字に騙されないようにしようの巻」vol19 2次関数 放物線の平行移動①ただし，二次関数の軸の方程式（頂点の x x x 座標）が必要になる機会はとても多いため， − b 2 a\dfrac{b}{2a} − 2 a b は覚えてしまうことをオススメします。 高校数学：2次関数の場合分け・軸が移動する場合 コメントを残す コメントをキャンセル メールアドレスが公開されることはありません。 * が付いている欄は必須項目です コメント * 名前 * メール * サイト * * 日本語が含まれない投稿は無視されますのでご注意ください。（スパム対策）

1

01センター試験２次関数 怜悧玲瓏 高校数学を天空から俯瞰する

数学Ⅰ 定期テスト対策2次関数場合分けのやり方について 2次関数場合分けのやり方について (ⅰ) 0 a 1 となってますが, 1はどこから出てきたのですか？ 2次関数 (関数y=ax2)・入試問題（高校入試）（中学3年生：第41回） 中学・数学数学が苦手な人、「計算はできるけど、文章問題ができない」という人が、今すぐやるべきことを3つにまとめて解説。 数学苦手だった僕もこれらのことを意識した結果 ここでは数学1の「二次関数」についてまとめています。 二次関数で学んだことは、それ以降に学習する様々な関数に対しても応用が可能です。 高校数学の関数全般の基礎となりますので、しっかり学習しておきましょう。 目次 1 1節 2次関数とそのグラフ 11 関数とグラフ 12 平方完成 13 2次関数のグラフ 14 グラフの平行移動 15 グラフの対称移動 16 2次関数の最大・最小 17 2次

世界一わかりやすい数学問題集中３ ４章 二次関数

最重要 軸 範囲が動く2次関数の最大値 最小値の場合分け解法パターン マスマス学ぶ

 2次関数とx軸の位置関係① ↑答えが分かったら画像をクリック↑ 2次関数とx軸の位置関係② ↑答えが分かったら画像をクリック↑ 2次方程式の解の公式 ↑答えが分かったら画像をクリック↑ 2次不等式① ↑答えが分かったら画像をクリック↑ よって2次方程式 \(x^22x1=0\) の解の個数は2個。解の正負も正が1個と負が1個とわかります。 言い忘れていましたが、2次方程式の解は2個以下になります。2次関数のグラフを見れば3個の共有点を持つことはあり得ませんよね。 では次の問題。\(2x^25x4=0\) の解 22次関数 最高次数が2の多項式で表される関数。 ① の時、下に凸。 の時、上に凸。 ② の時、最小値がある。 の時、最大値がある。 ③ 頂点は 。 ④ 軸 に対して線対称。 ⑤ の時の二次方程式の解は、 軸と交わる座標。

2次関数 媒介変数 スタディーx

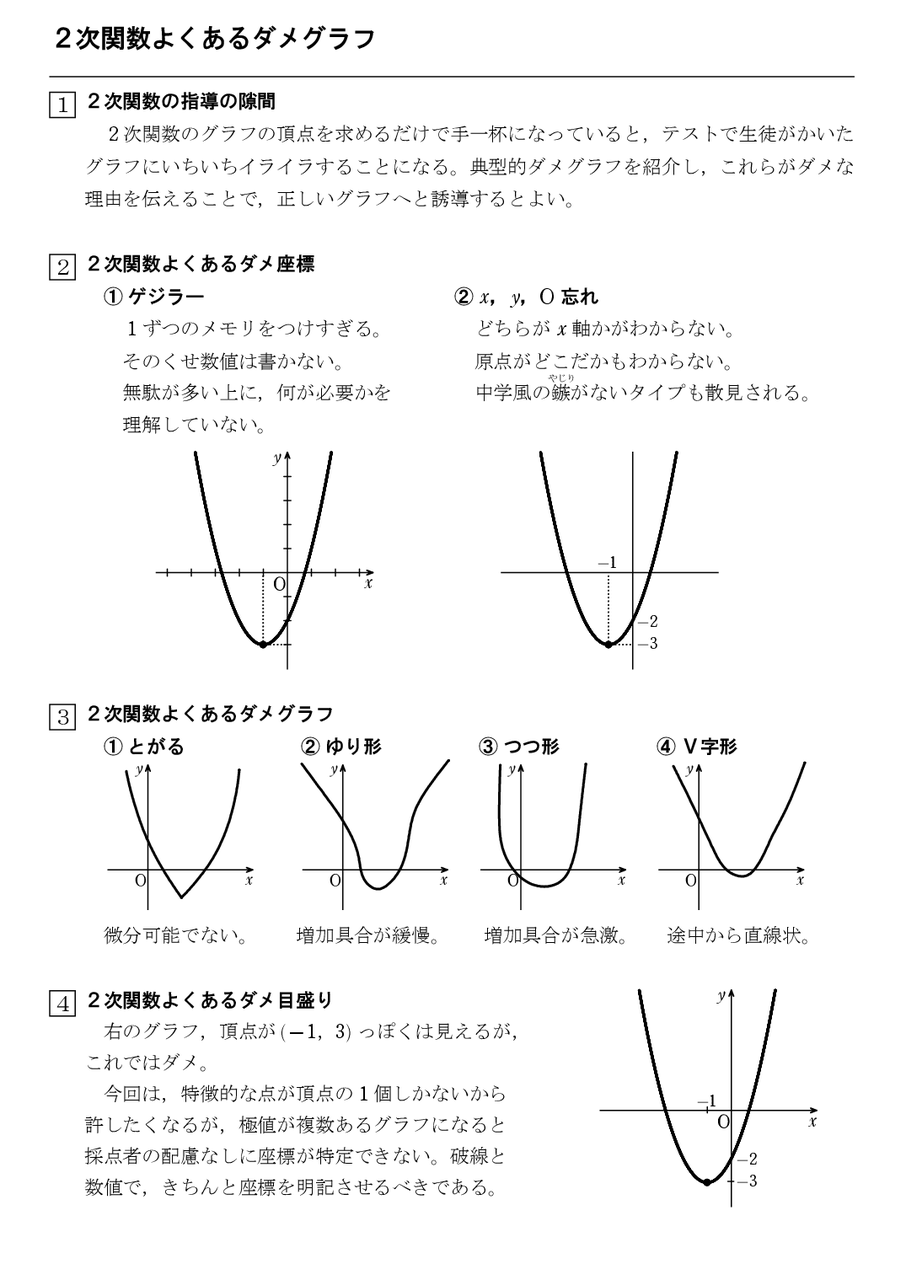
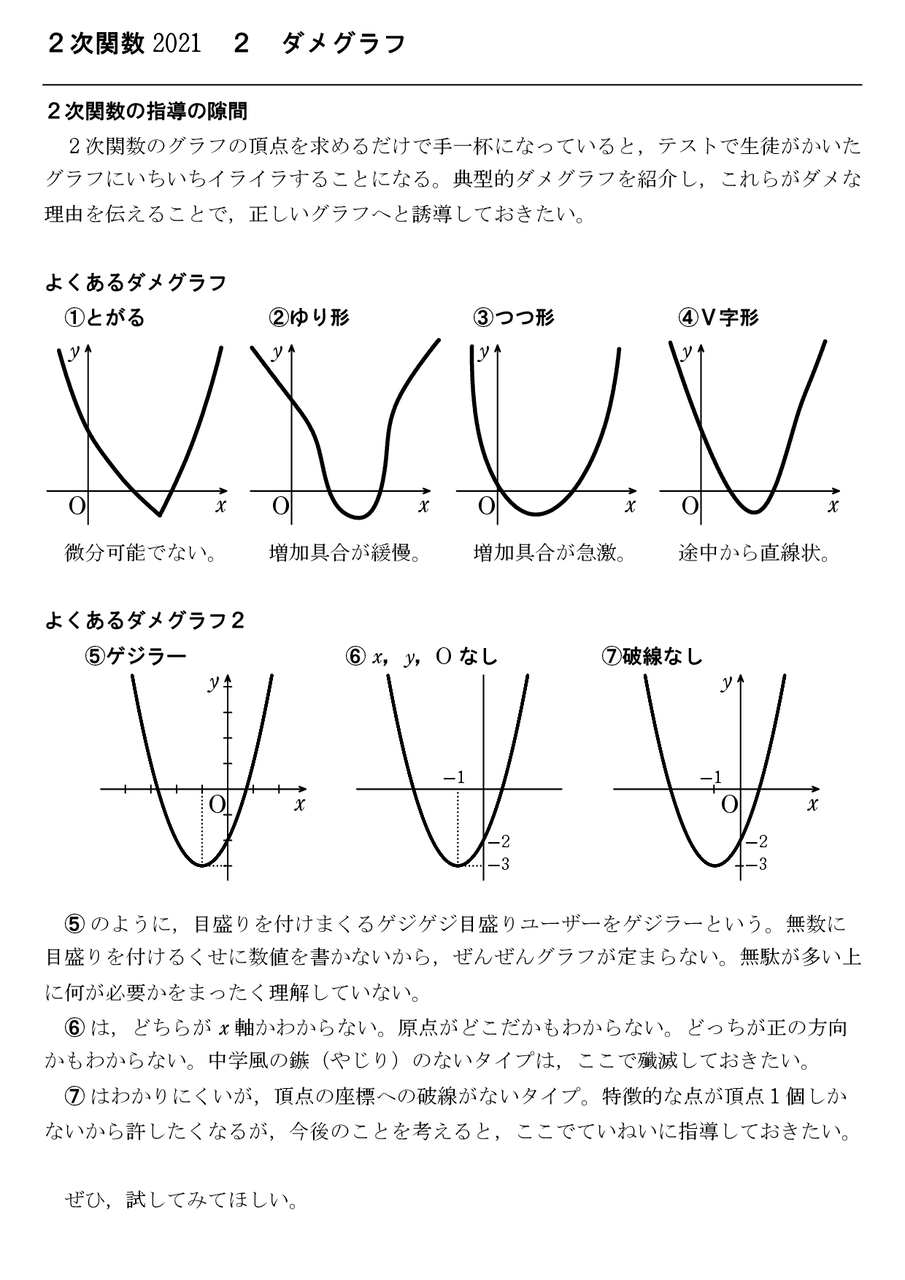
２次関数よくあるダメグラフ 怜悧玲瓏 高校数学を天空から俯瞰する

第1章 2次関数1．2次関数のグラフ 第1章 2次関数 1．2次関数のグラフ 2次関数のグラフを学習します． y= ax2 y = a x 2 から始めて， y= ax2q y = a x 2 q, y= a(x−p)2 y = a ( x − p) 2 とたどり， y =a(x−p)2q y = a ( x − p) 2 q のグラフを見ます． それぞれにおいて数学Ⅰ 定期テスト対策2次関数f (x)の意味 2次関数 f ( x )の意味 関数の式の中に， f ( x ) や f (－1) が出てきますが，この意味がわかりません。一般形 f(x) = ax 2 bx c は多項式の一般論を適用するときに便利であり、標準形 f(x) = a(x p) 2 q や因数分解形 f(x) = a(x s)(x t) は座標平面上に描かれる放物線を通して二次関数の性質を調べるときに便利な形である。 y = a(x p) 2 q の形で表される xy平面上の放物線の軸は x = p であり、

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

中学３年生 数学 ２次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

 また、 「2次関数」の単元は高校数学ではとても大切な単元 です。 基本的に関数が絡むと、この 2次関数に帰着させる ことが多くなります。 ですから、2次関数についての知識はたくさん持っていた方が良いでしょう。 そのような「2次関数」の単元ですが、まずは導入として中学で学習した関数を中心に学習しましょう。 目次 1 関数の式とグラフ 11 関数の定義 12 2つの変数の関係関連記事 高校数学 解説動画 数学Ⅱ 図形と方程中学校数学 2次関数の変域の問題の解き方・ポイントを解説 管理人 4月 29, 2次関数の問題にはいくつか種類がありますが、代表的なものの一つに『変域』の問題があります。 変域は比例や1次関数の単元でも習ったと思います。 基本的な考え方は変わらないのですが、2次関数ならではの

高校数学 数 ４９ ２次関数の決定 Youtube

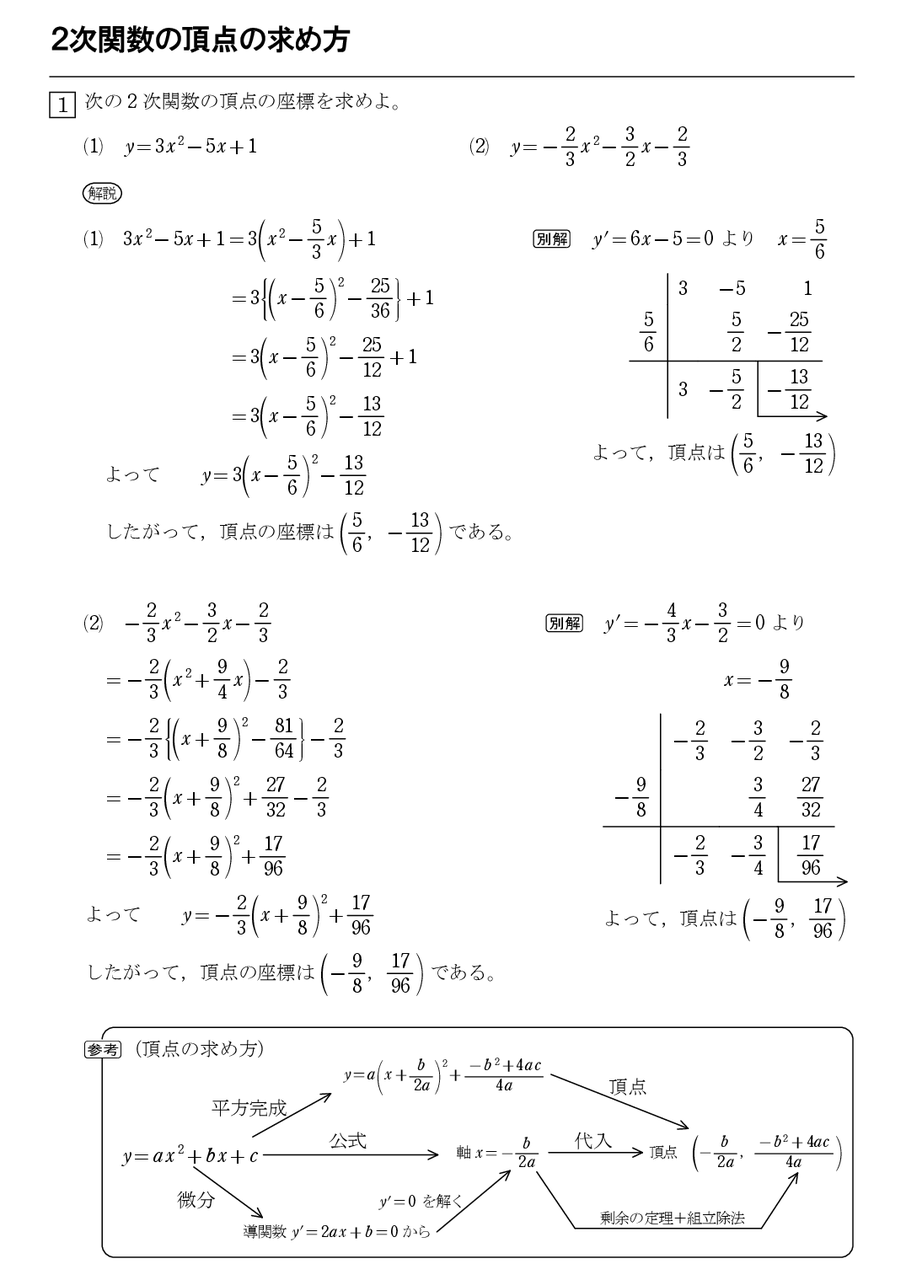
２次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する

数学Ⅰ 2次関数 復習 復習 解の公式を使う 過去問解説 大学入学共通テスト 22本試 数学ⅠA 第1問 3 22本試 数学ⅠA 第2問 1 21本試 数学ⅠA 第1問 1 21本試 数学ⅠA 第2問 1 21追試 数学ⅠA 第2問 1 18問題例 記述式を含む 問題例2 1 18問題例 記述式を含む 問題例1 2 18試行調査 数の二次式で表す事ができる関数を変数 の 2次関数 という。 具体例 以下の関数はいずれも2次関数である。 ( 、 、 の場合に相当) ( 、 、 の場合に相当) ( 、 、 の場合に相当) 一方以下の関数は2次関数では ない 読者はこれを当然と思うかもしれないが、上の式は と表記することもできる。 しかし、これは 二次式ではないので2次関数ではない。 そのために、2次関数の定義において でなければならない 数学Ⅰ 2次関数 2次関数の決定特訓② ＜最大・最小・平行移動＞ 解答編 ＜直線上に頂点＞ 数学Ⅰ 2次関数 2次関数の決定特訓③ ＜直線上に頂点＞ 問題編 数学Ⅰ 2次関数 2次関数の決定特訓③ ＜直線上に頂点＞ 解答編 スポンサードリンク Tweet;

二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局

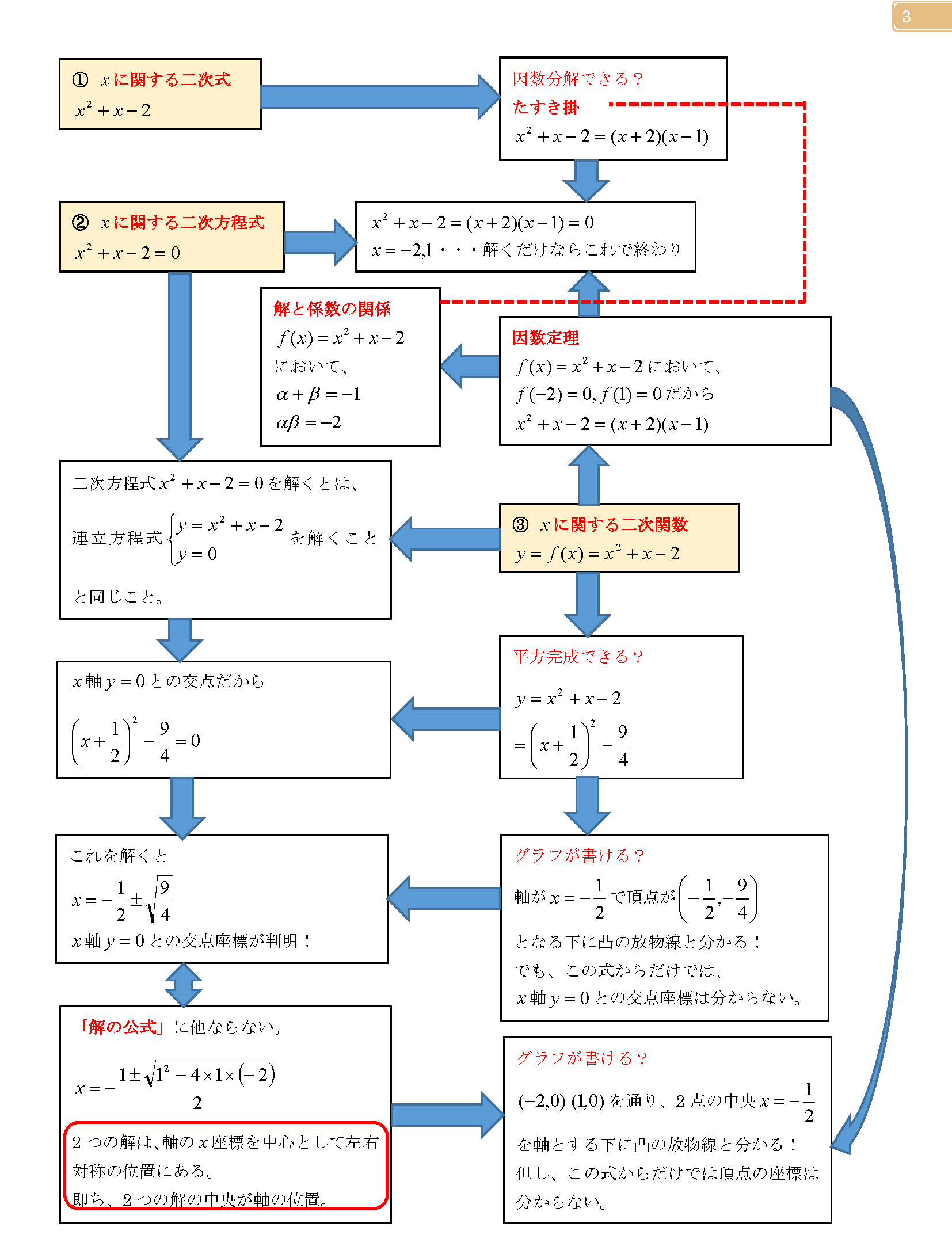
二次式 二次方程式 二次関数が分からん 数学を苦手にさせたのは誰 夏期講座超初級1 勉強法のバイブル 帝都大学へのビジョン

MathAquarium練習問題2 次関数 2 2 (1) 放物線y＝－2x2－14x－13 をどれだけ平行移動すると，放物線y＝－2x2＋8x＋7 に重なるか。 (2) 2 次関数y＝x2＋ax＋4 のグラフを，x 軸方向に2 だけ平行移動すると2 次関数y＝x2－9x＋b の グラフとなる。このとき，a，b の値を求めよ。 数学I次関数の応用問題 数学IAIIB Twitter Facebook はてブ Pocket LINE コピー 差をつける自宅学習を始めよう ここでは2次関数に関する応用問題を解説します。 様々な問題を解くことによって，それぞれの問題の考え方を身に付けましょう。 Contents 1 2変数関数の最小値を求める問題;2次関数とは、「2次の関数」、つまり「変数の次数が2の関数」を指します。 2次 関数を表す式：y = ax2 y = a x 2 比例を表す式は y = ax y = a x で x x は1次でしたが、この x x が2次になったものが2次関数です。 比例の場合、 「y y がx x に比例する」 と言いましたが、2次関数の場合は 「y y がx2 x 2 に比例する」 と言います。 x x を 倍したとき、y y も 倍になる関係が比例 x x を 倍したとき、y y

大学入試共通テスト数学の裏技 2次関数の最大 最小は 頂点と区間の端を調べよ 受験の月

18 センター数学 ａ ２次関数を瞬殺する 怜悧玲瓏 高校数学を天空から俯瞰する

このページでは、 数学Ⅰ「2次関数」の教科書の問題と解答、公式をまとめています。 教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。 また、平方完成・平行移動の問題もわかりやすく解説しています。 目次 1 教科書 問題と解答一覧 2 公式一覧 3 平方完成・平行移動の問題解説 1 教科書 問題と解答一覧 教科書（数学Ⅰ）の「210大学入試センター試験数学Ⅱ・B解説 09大学入試センター試験数学Ⅰ・a解説 09大学入試センター試験数学Ⅱ・B解説 その他年度や分野別入試問題はこちらから 2次関数 2次不等式 2次不等式の解法 例題 練習問題 2次式での定符号の条件① 例題 練習問題 2次式での定符号の条件② 例題

中学3年数学 二次関数 二次関数では必須の平方完成 やり方と成り立ちをわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト

中学3年の数学 動画 二次関数のグラフ の問題 19ch

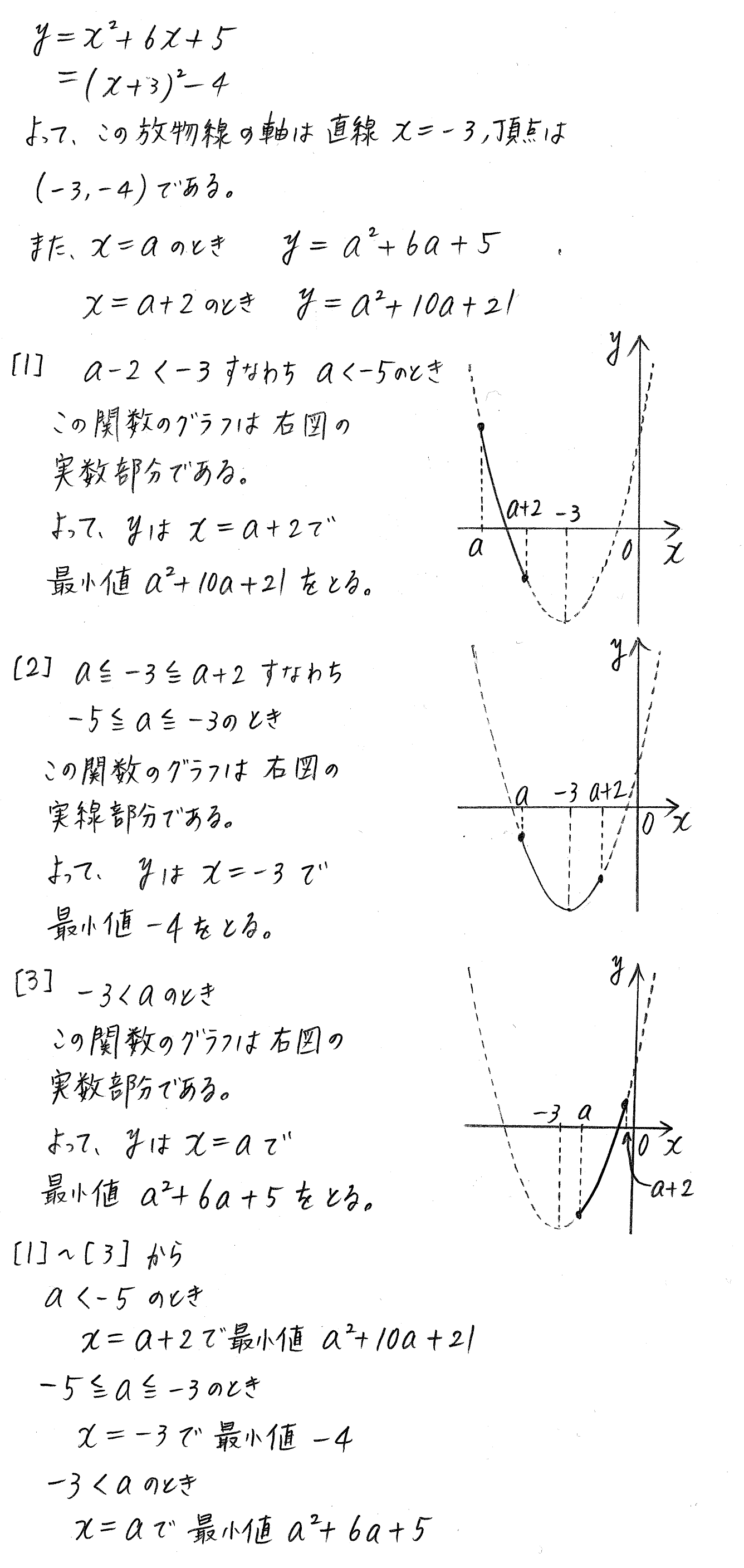
改訂版 クリアー数学 P47 15 ２次関数の最大 最小

数学 2次関数の最大 最小 2次関数の決定 高校1年生 教科書練習問題 赤城 ᐡᐤᐡ

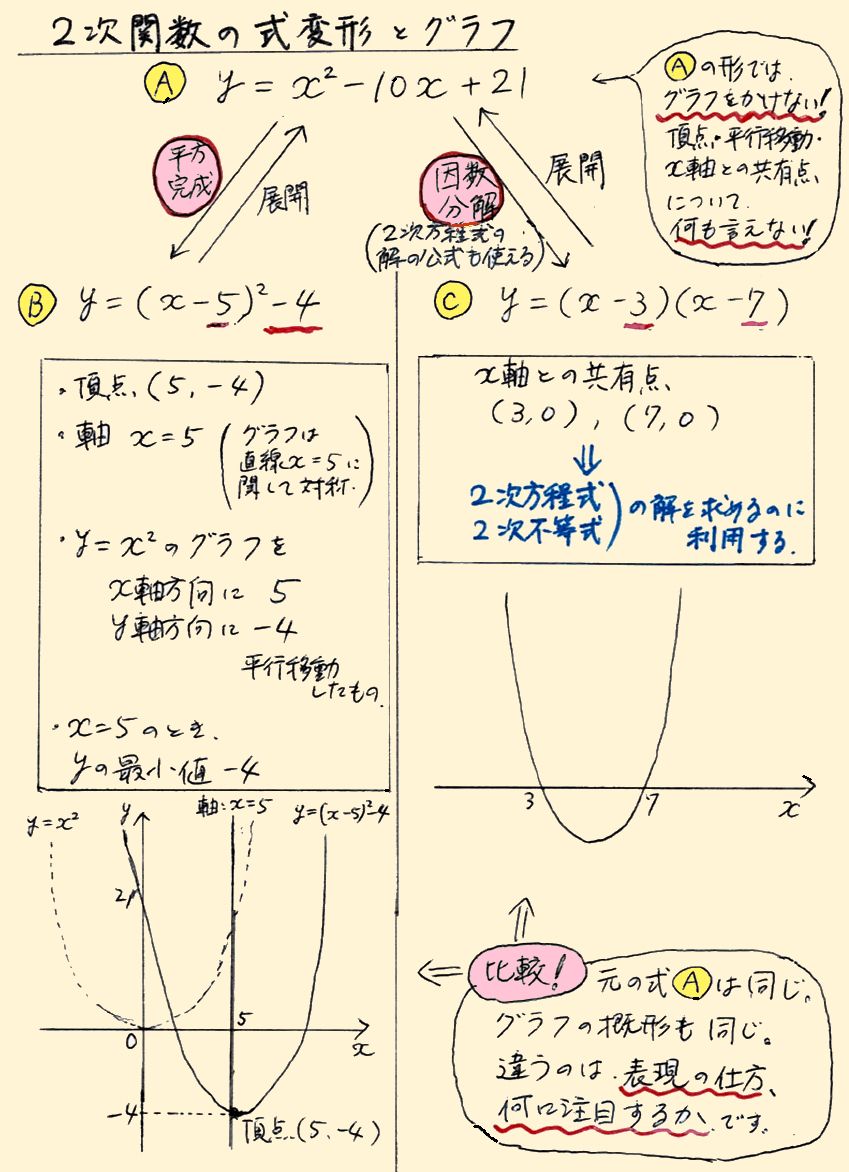
数学 ２次関数 目的をもった式変形を 温故知新の勉強法 温故知新ラーニング 楽天ブログ

２次関数の移動に関する問題まとめ チャート 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

都立入試数学 二次関数 大問３ 二乗に比例する関数のひみつ 都立高校入試で成功する方法

中学数学問題集 中３ ２次関数 １８ 4 中学数学高校数学個別指導in山形市 数専ゼミ

数学の二次関数の問題で 空欄部分がわかりません グラフと回答を教えて下さい Clearnote

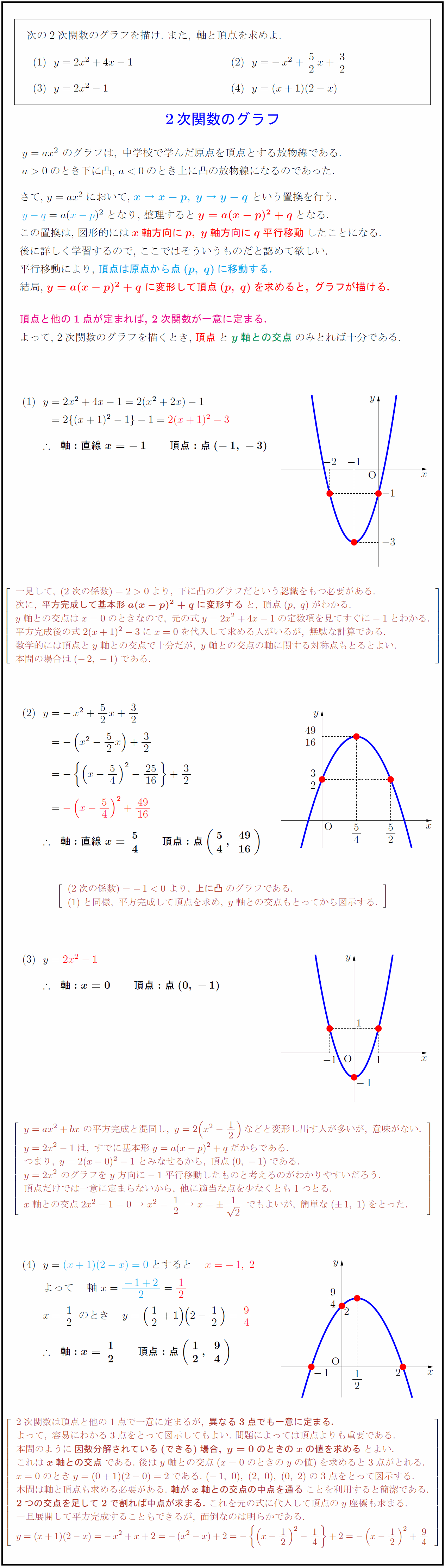
高校数学 2次関数y Ax Bx Cのグラフ 受験の月

1

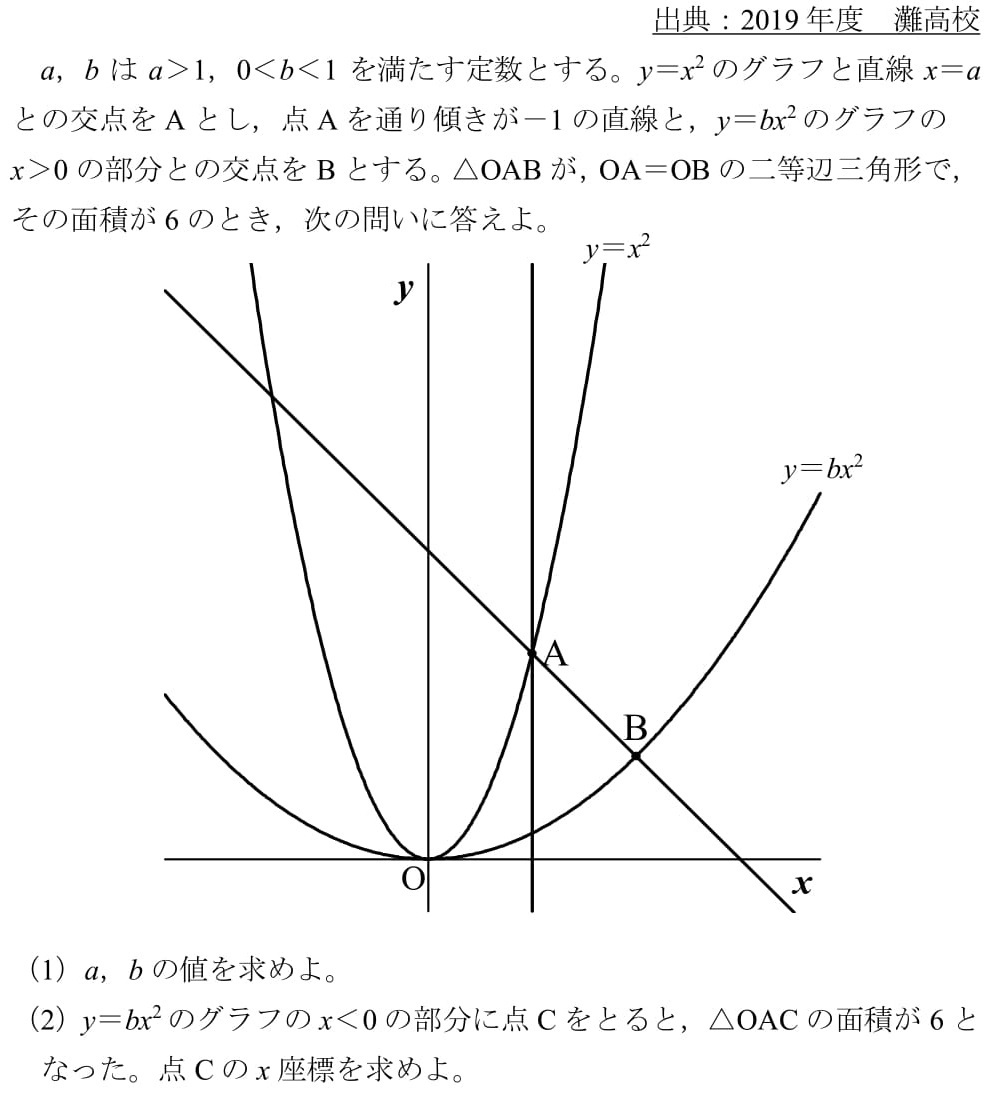
中点とy Xに対称 19年度灘高校 高校入試 数学 良問 難問

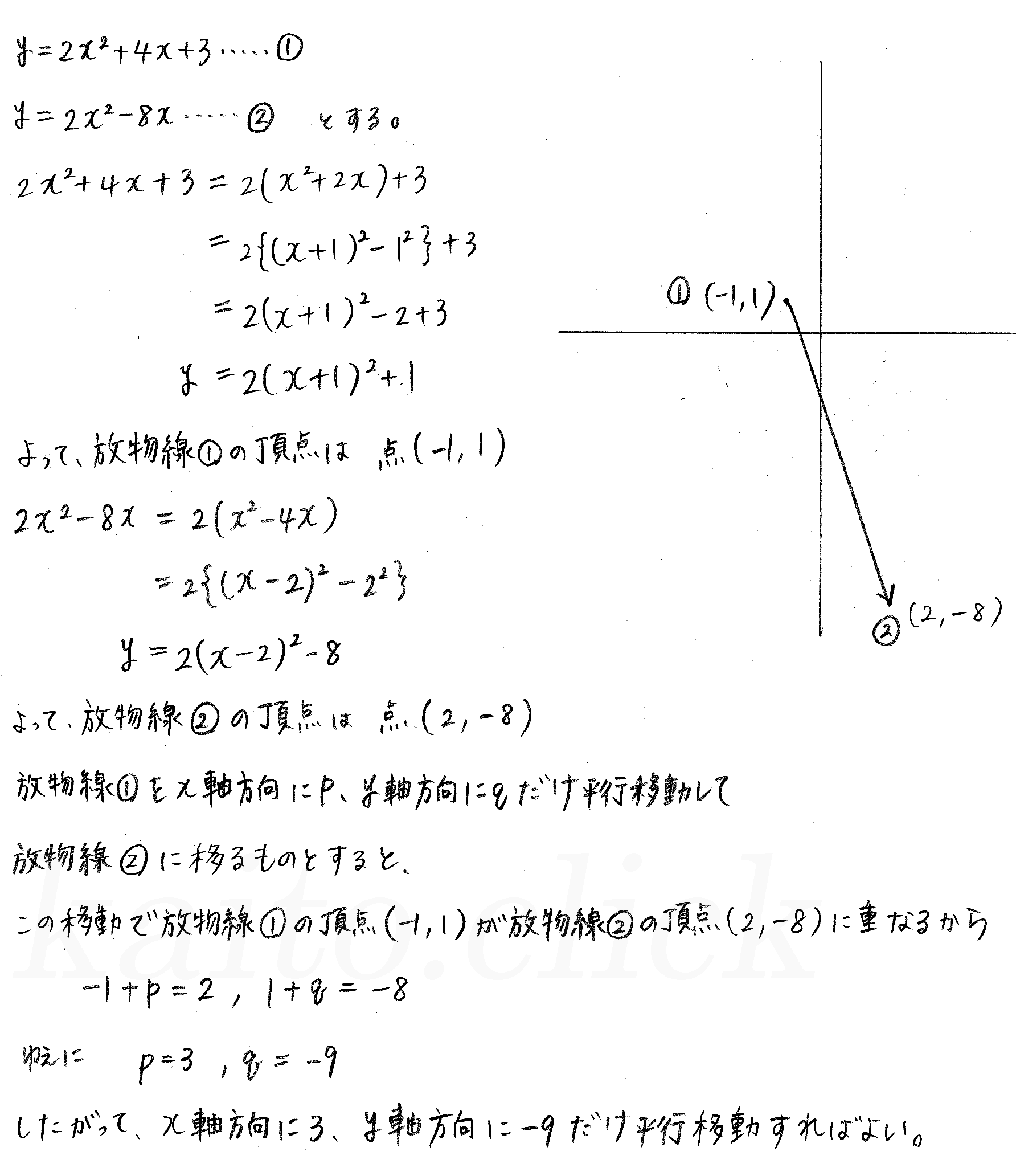
改訂版 クリアー数学 P41 14 ２次関数のグラフ

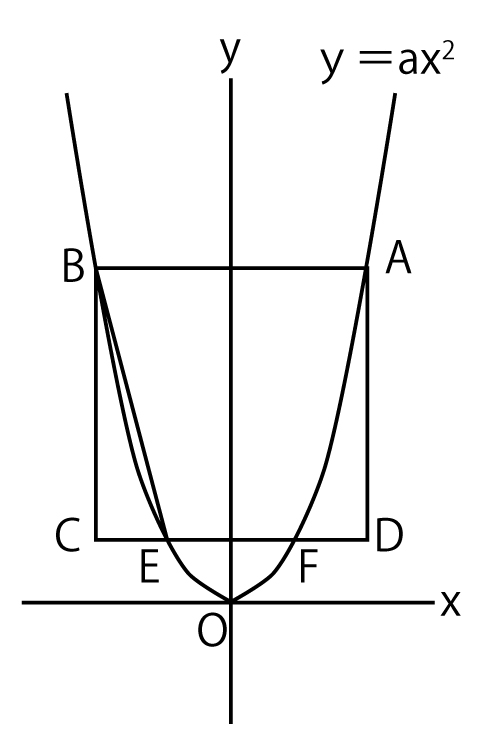
12年前期 千葉県公立高校入試 数学 第4問 二次関数 配点計10点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

都立高校入試数学 2次関数 対策 坂本良太 都立専門 本質の勉強法を伝える受験講師 Note

中学３年生 数学 ２次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

二次関数とグラフ 中３数学 高校数学 Irohabook

高校数学 ２次関数 教科書 問題 解答 公式 解説 学校よりわかりやすいサイト

中学3年の数学 動画 二次関数の利用 一次関数とのコラボ編の問題 19ch

高校数学 2次関数がx軸から切り取る線分の長さ 受験の月

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

世界一わかりやすい数学問題集中３ ４章 二次関数

高校数学 数 ５０ ２次関数の決定 Youtube

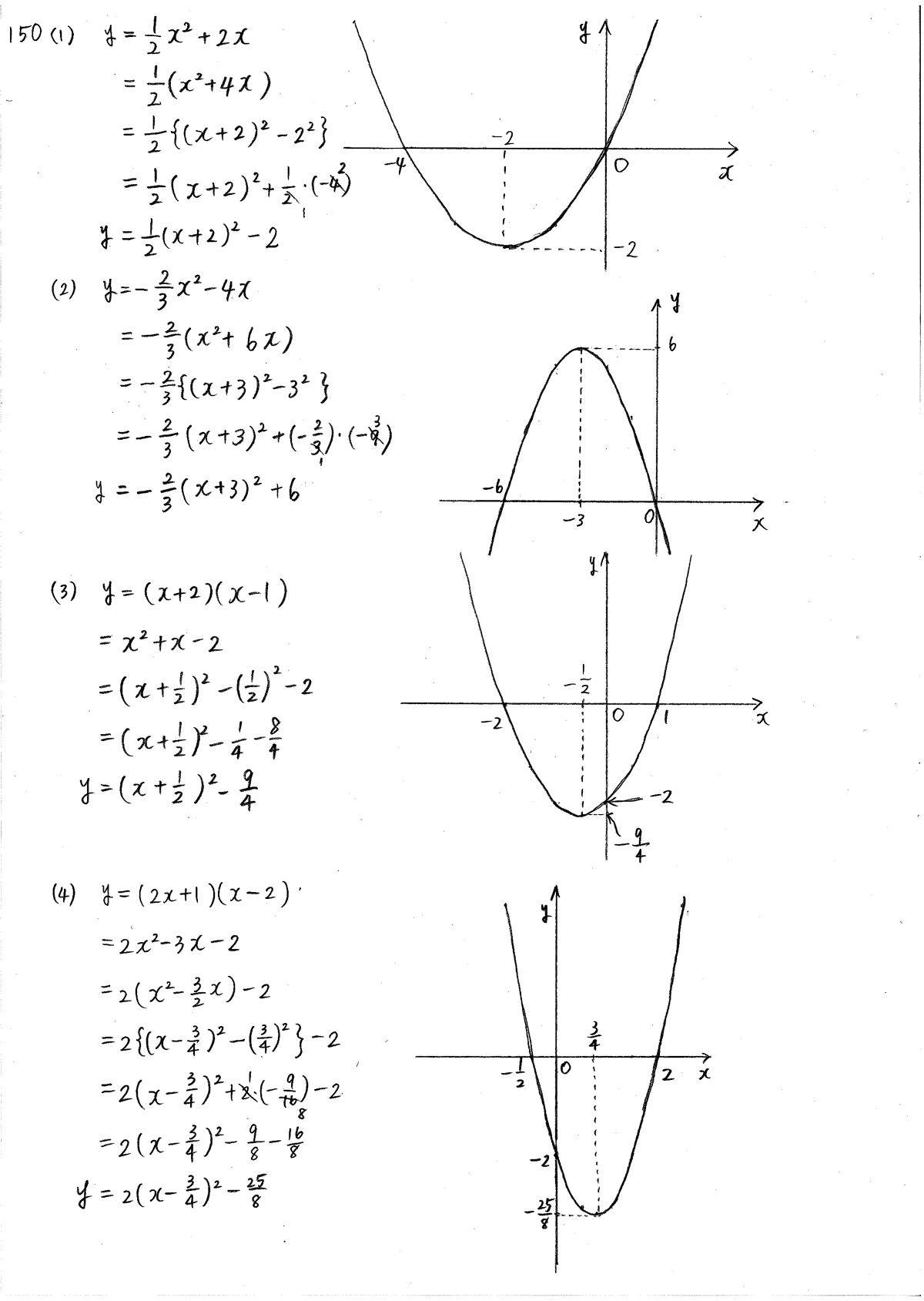
クリアー数学 数1 P39 15 ２次関数のグラフ

２次関数 2次不等式の解法 数学 定期テスト対策サイト

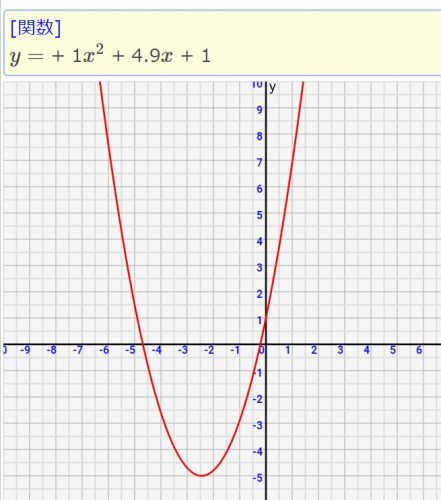
二次関数をシミュレーション 図解で理解 数学入門

数学 中3 35 二次関数のグラフ Youtube

原田 浩明 Sサクシード099 二次関数を置き換えて その最大値最小値で 置き換えた文字の範囲を考える 高校 数学 二次関数 最大最小 T Co Svks8odlqb Twitter

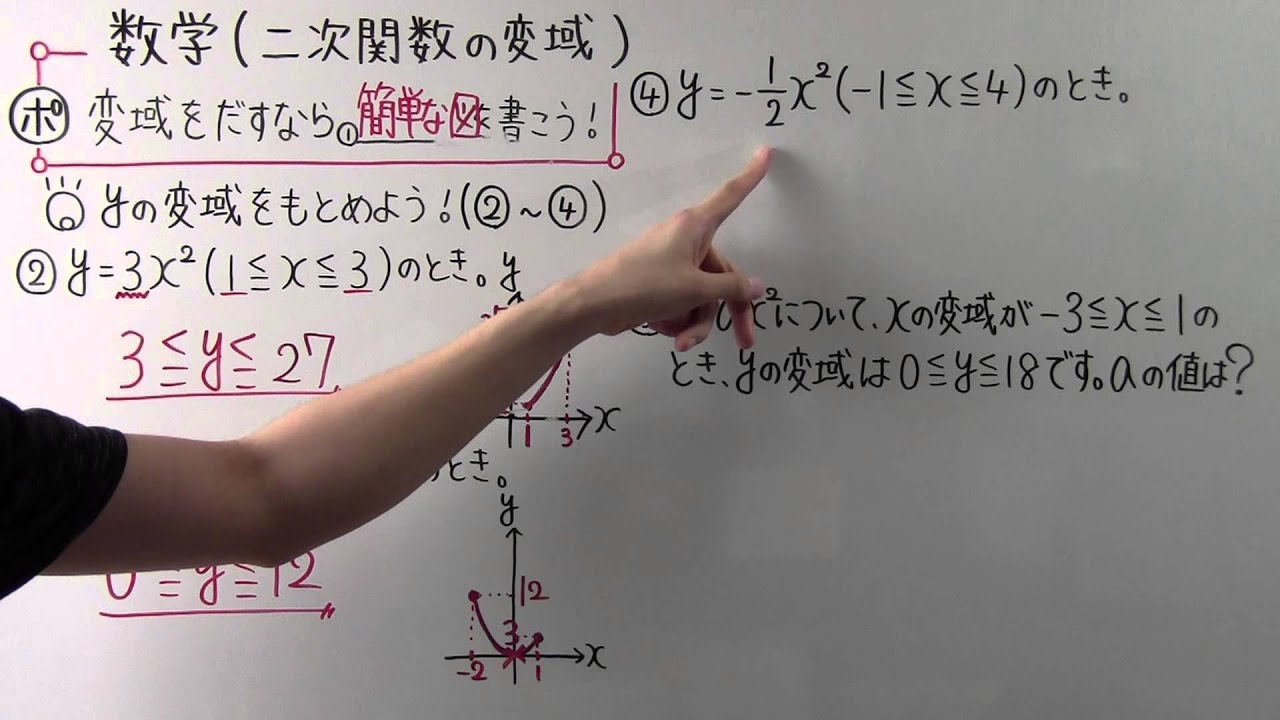
数学 中3 37 二次関数の変域 Youtube

高校数学 2つの2次関数の間の面積と裏技a 6公式 受験の月

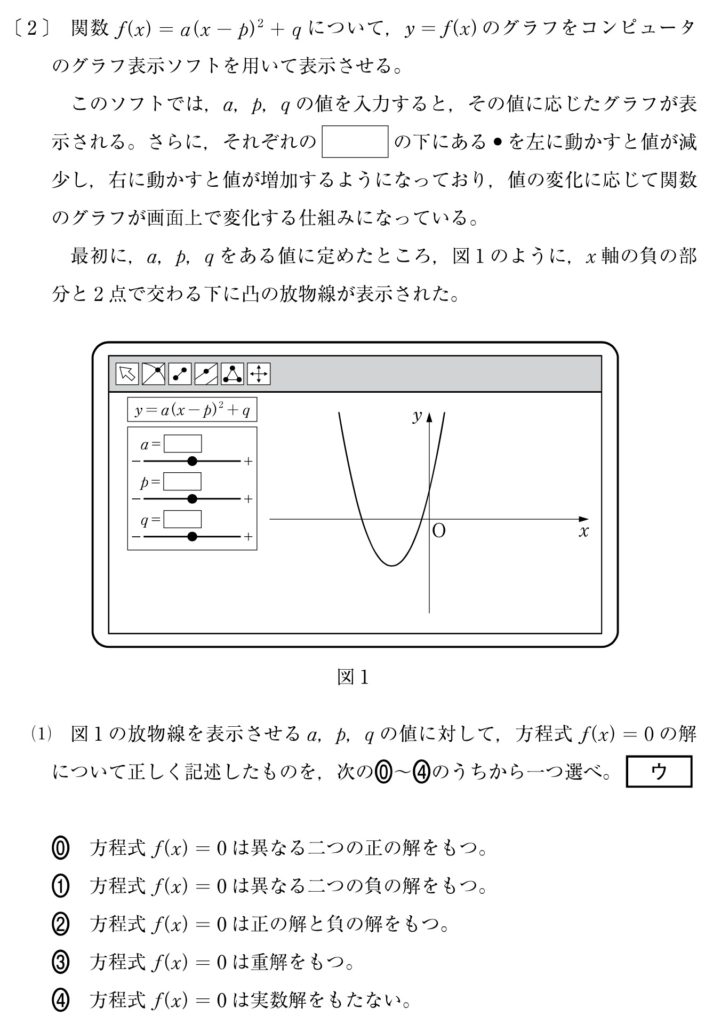
共通テスト プレテスト 数学 Ia を一挙解説 スタディクラブ情報局

中学３年生 数学 ２次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

２次関数 怜悧玲瓏 高校数学を天空から俯瞰する

９月１２日更新 中３数学 二次関数の応用有名問題 成績 上がってます 根城学習塾 八戸市

二次関数の基本 現役塾講師のわかりやすい中学数学の解き方

1講 2次関数の最大 最小 2章 2節 2次関数の値の変化 問題集 高校数学

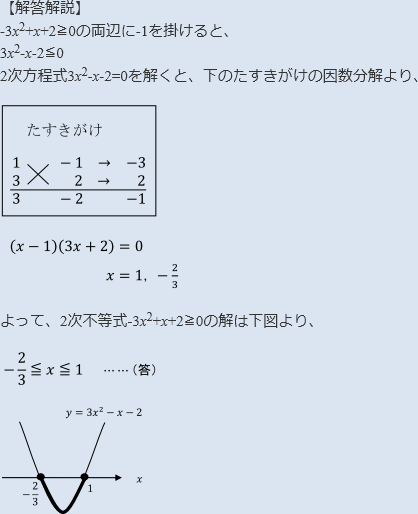
２次関数 2次不等式の解法 数学 定期テスト対策サイト

数学質問 二次関数と三角形の面積 Youtube

解の公式

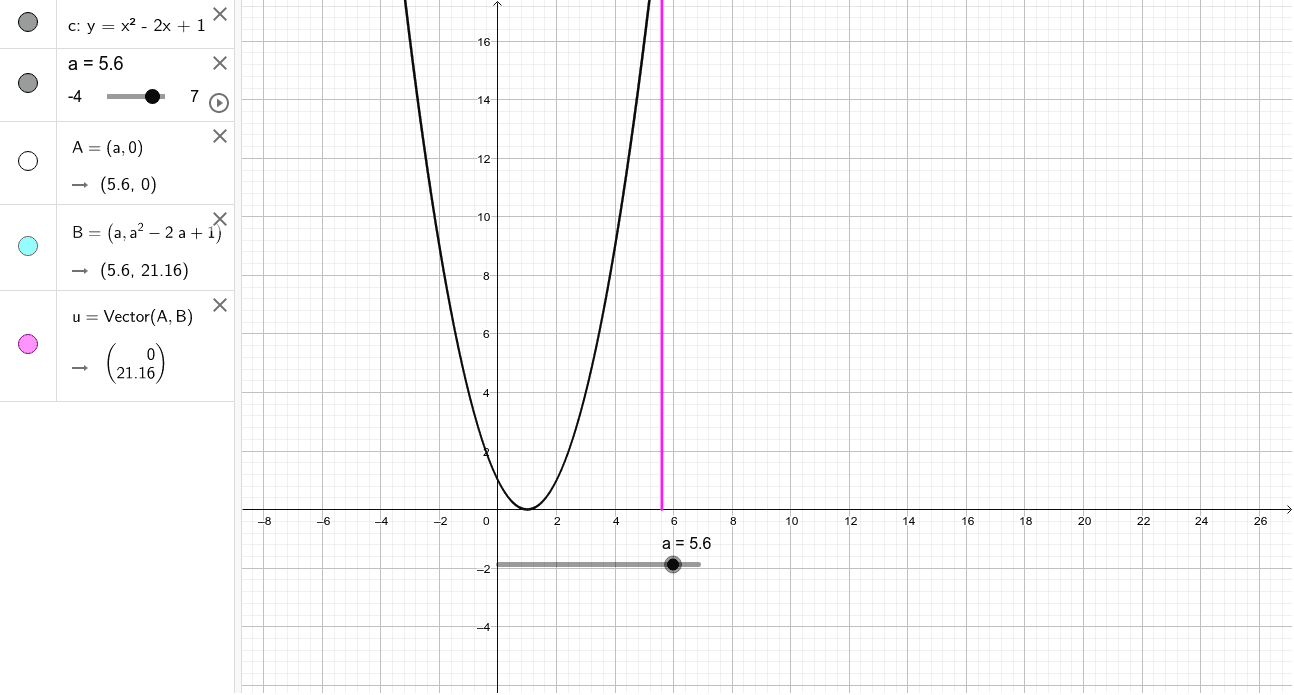
数学i 2次関数の符号 2 Geogebra

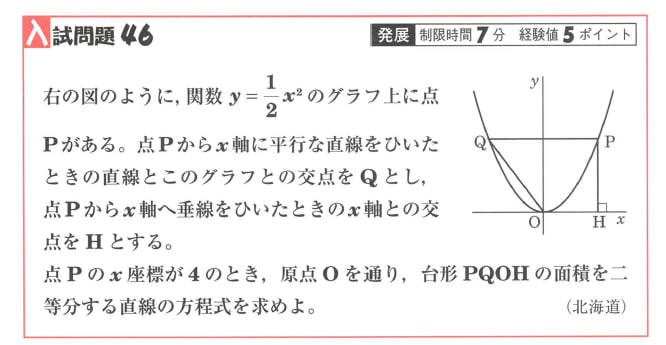
中学数学 １次関数 ２次関数 46 北海道 宮城県 高校入試問題 英語 数学 さくら教育研究所 中学 高校受験 Skredu

中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su

高校受験 数学テーマ別攻略 二次関数と直線 日比谷高校のススメ

中3数学 二次関数15 関数y Ax 2の利用 図形の移動 すべて無料 星組の中学数学講座

2次関数の最大 最小 数学i フリー教材開発コミュニティ Ftext

16年前期 千葉県公立高校入試 数学 第3問 二次関数 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

高校数学 ２次関数 平方完成の練習 学習プリント集

高校数学 2次関数の場合分け 定義域が動く 数樂管理人のブログ

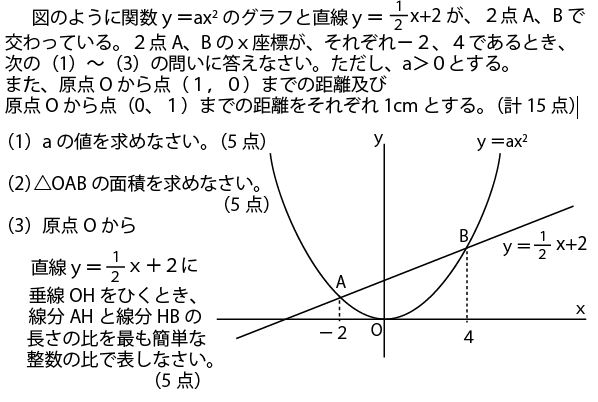
17年前期 千葉県公立高校入試数学 第3問 二次関数 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

中学数学問題集 中３ ２次関数 １９ 2 中学数学高校数学個別指導in山形市 数専ゼミ

高校数学 数 35 ２次関数 Youtube

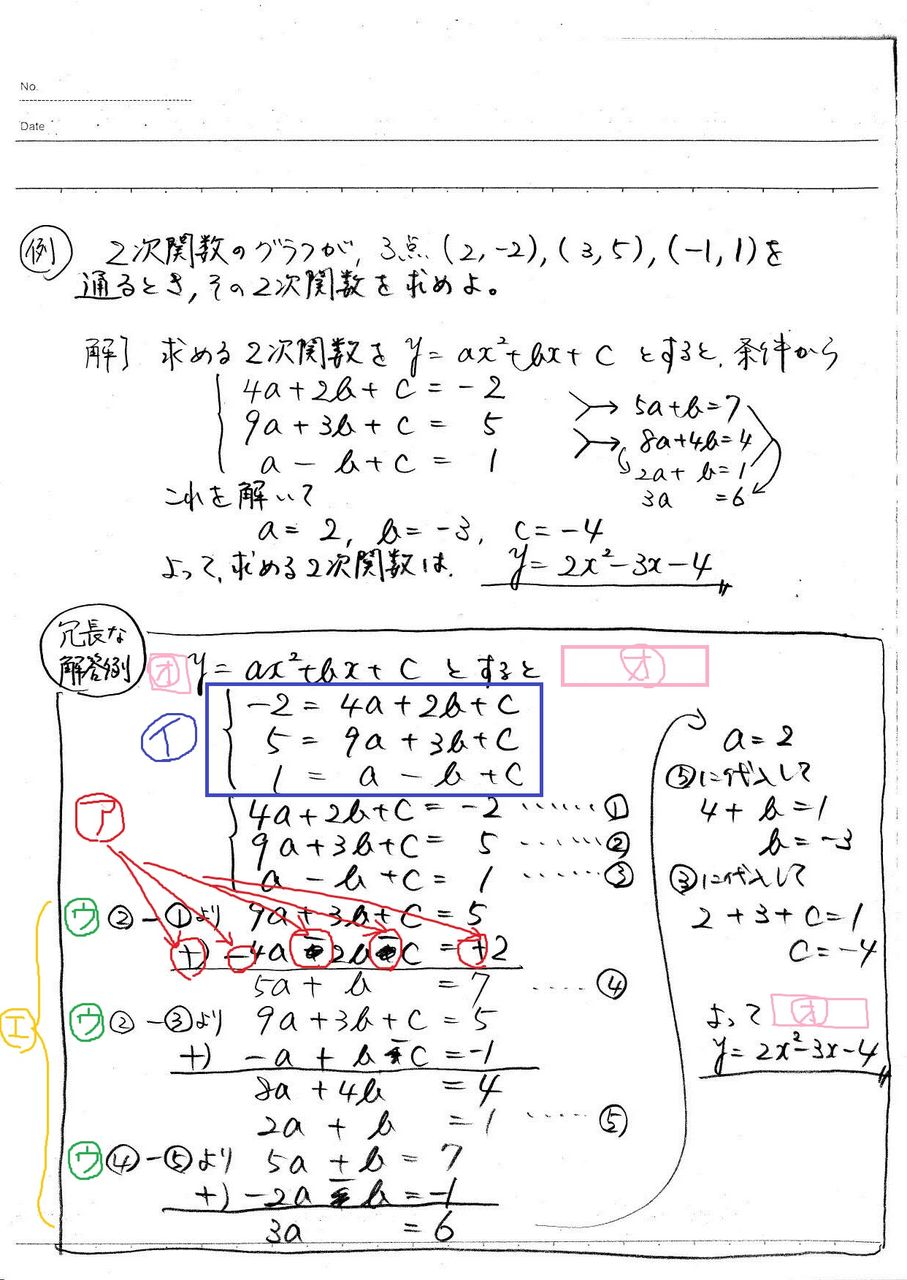
２次関数のグラフ 研究授業ネタ３ 怜悧玲瓏 高校数学を天空から俯瞰する

高校数学 関数は グラフが命 映像授業のtry It トライイット

中3数学 二次関数クルクル回る問題 ブログ アビット

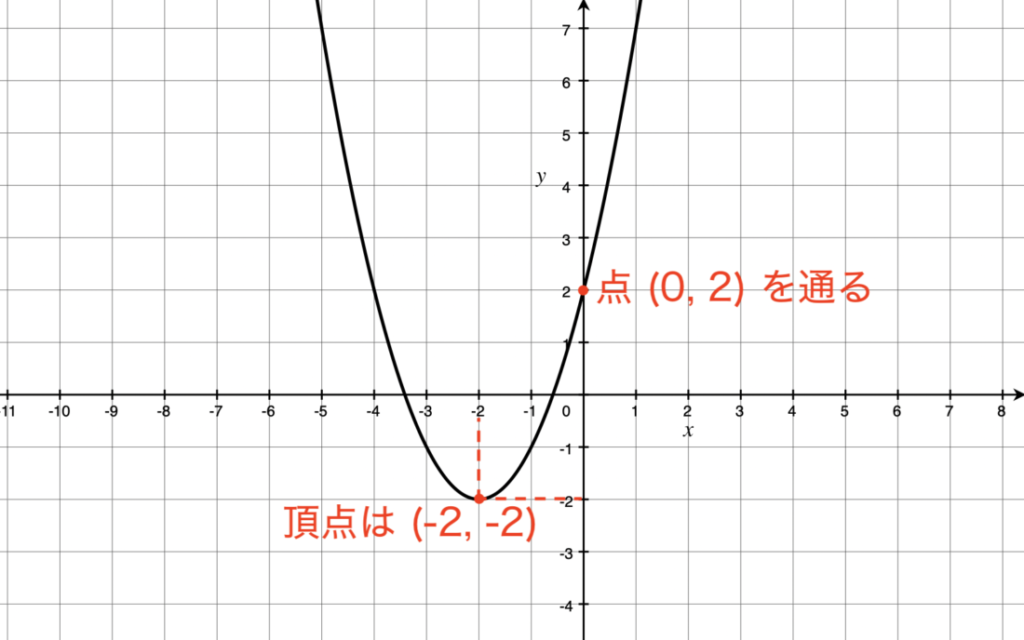
二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局

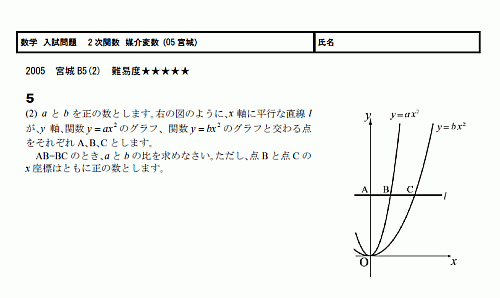
2次関数 媒介変数 スタディーx

2次方程式と2次関数の関係 数学i フリー教材開発コミュニティ Ftext

中学数学の２次関数 Y A X 2 大垣日本大学高校の入試問題を解く 身勝手な主張

2次方程式から2次関数を考える 数学i フリー教材開発コミュニティ Ftext

２０１７年 東大理系数学 第５問の解説 二次関数 二次曲線 放物線 接線 判別式 日本で唯一の東大文系 完全 特化 オンライン 東大合格 敬天塾

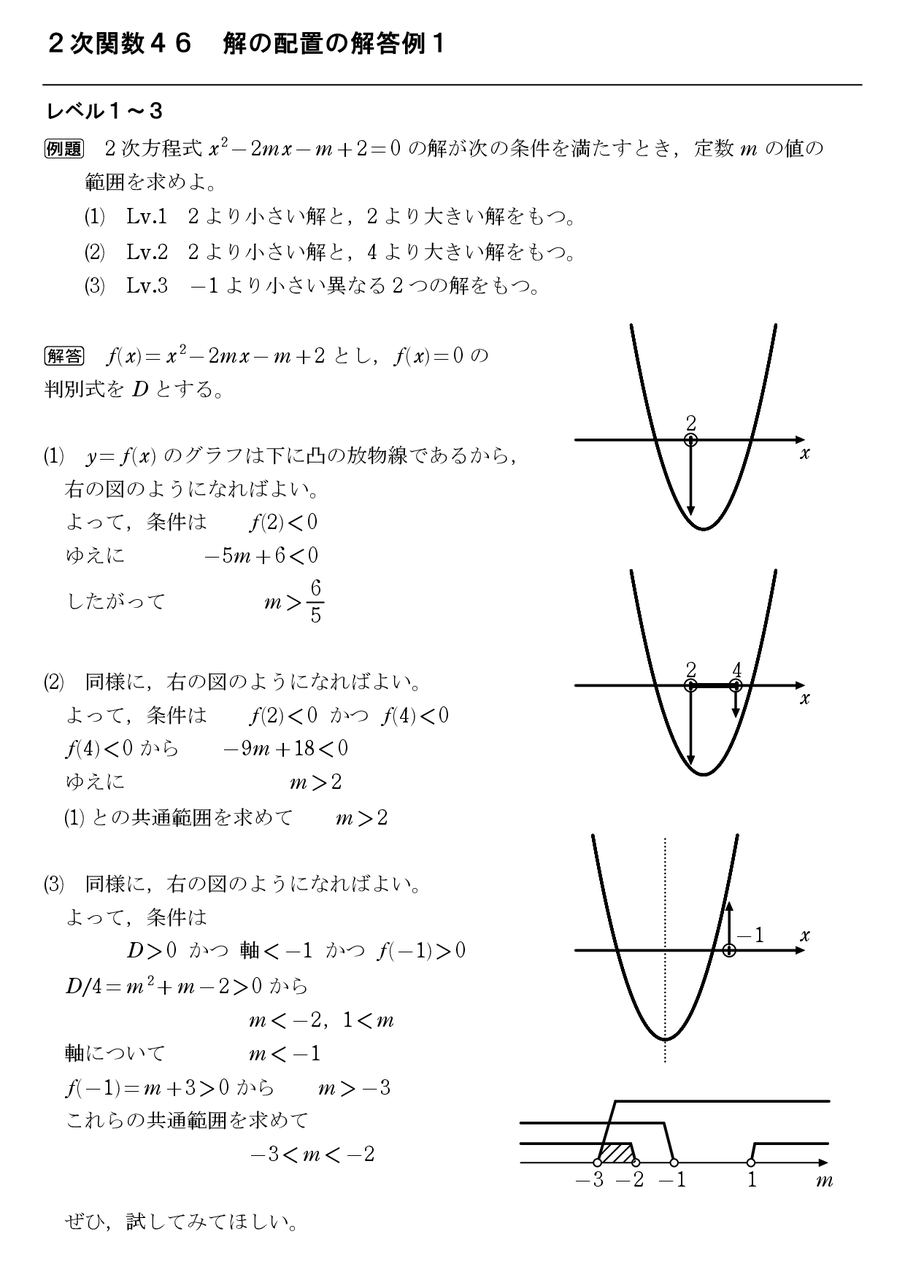
２次関数４６ 解の配置の解答例１ 怜悧玲瓏 高校数学を天空から俯瞰する

二次関数の利用 現役塾講師のわかりやすい中学数学の解き方

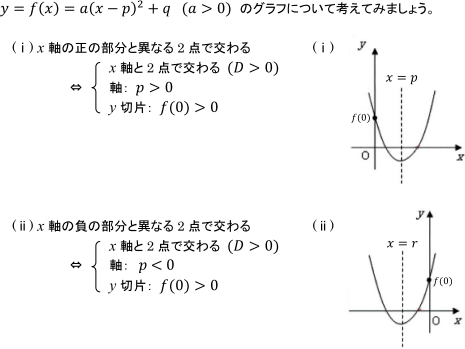
２次方程式の解の存在範囲と判別式 高校数学 定期テスト対策 ベネッセ教育情報サイト

２次関数のグラフ

1

数学1 2次関数勉強法 センター数学頻出の2次関数をマスターするポイント

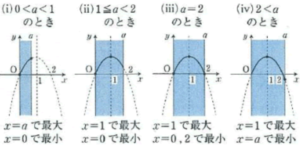
数学 二次関数 で絶対に抑えておくべきポイント3選 大学受験のseras学院 茨木校

２次関数とその応用 英語 数学 さくら教育研究所 中学 高校受験 Skredu

高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット

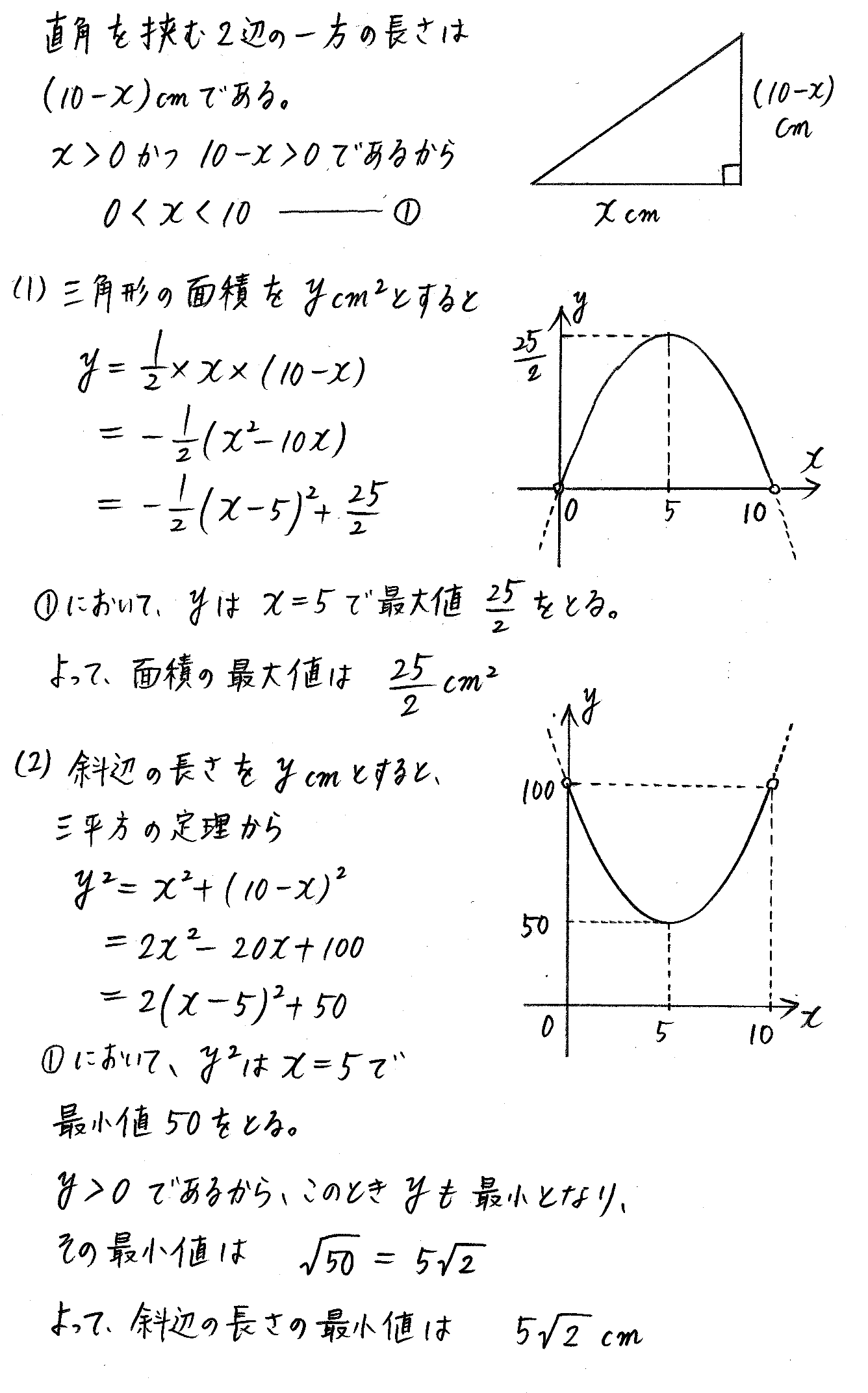
改訂版 クリアー数学 P48 15 ２次関数の最大 最小

中学３年生 数学 ２次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月

中３数学 ２次関数 原点に頂点がない三角形の面積の求め方 トルテン

二次関数 Wikipedia

３trial数学１ 3trial数1 P38 ３ ２次関数の最大 最小

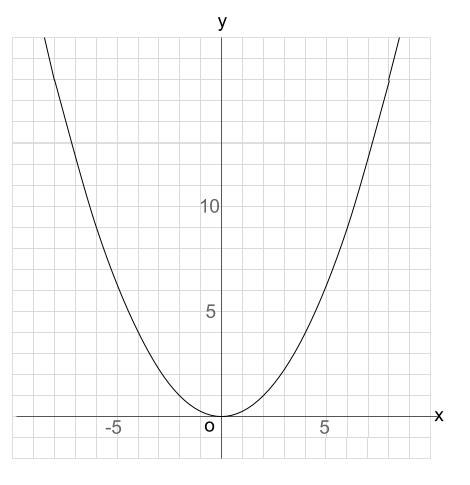
中学数学 Y Ax 2 のグラフを読み取る 中学数学の無料オンライン学習サイトchu Su

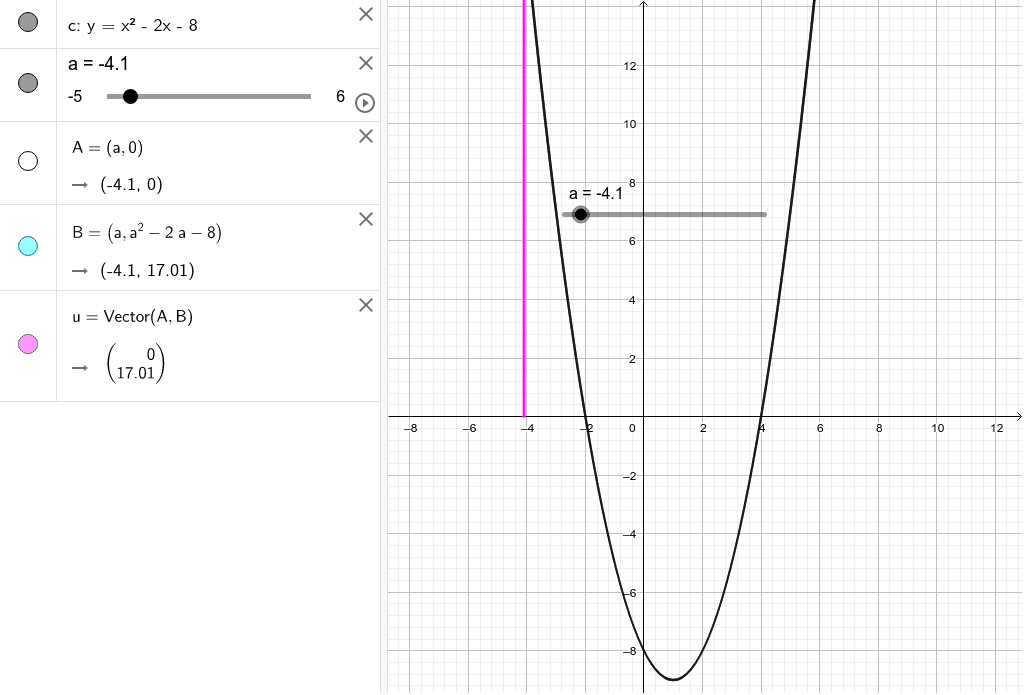
数学i 2次関数の符号 1 Geogebra

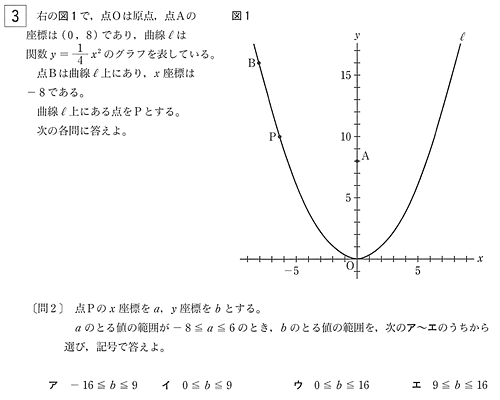
数学 二次関数のひっかけ問題 高校受験ブログ 学校が言えないノウハウ

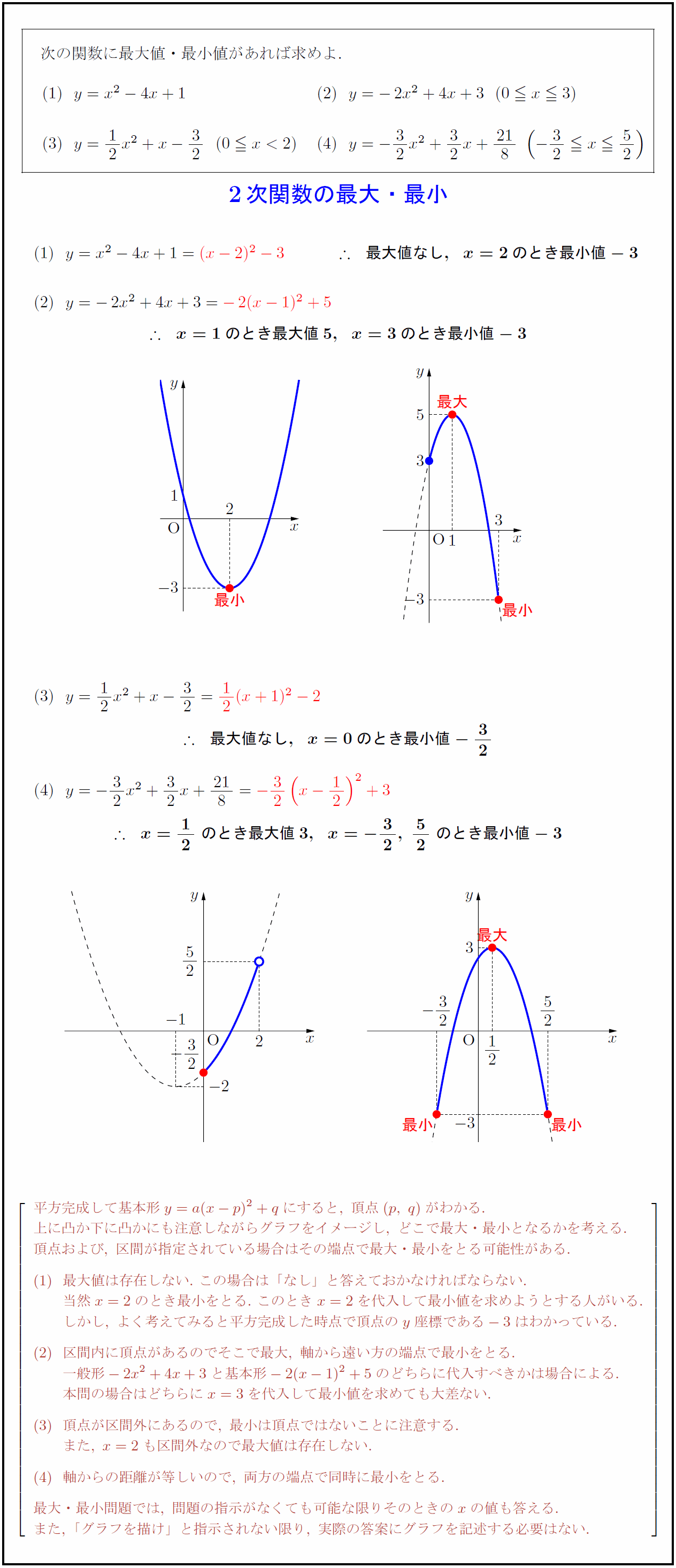
高校数学 2次関数の最大 最小の基本 受験の月

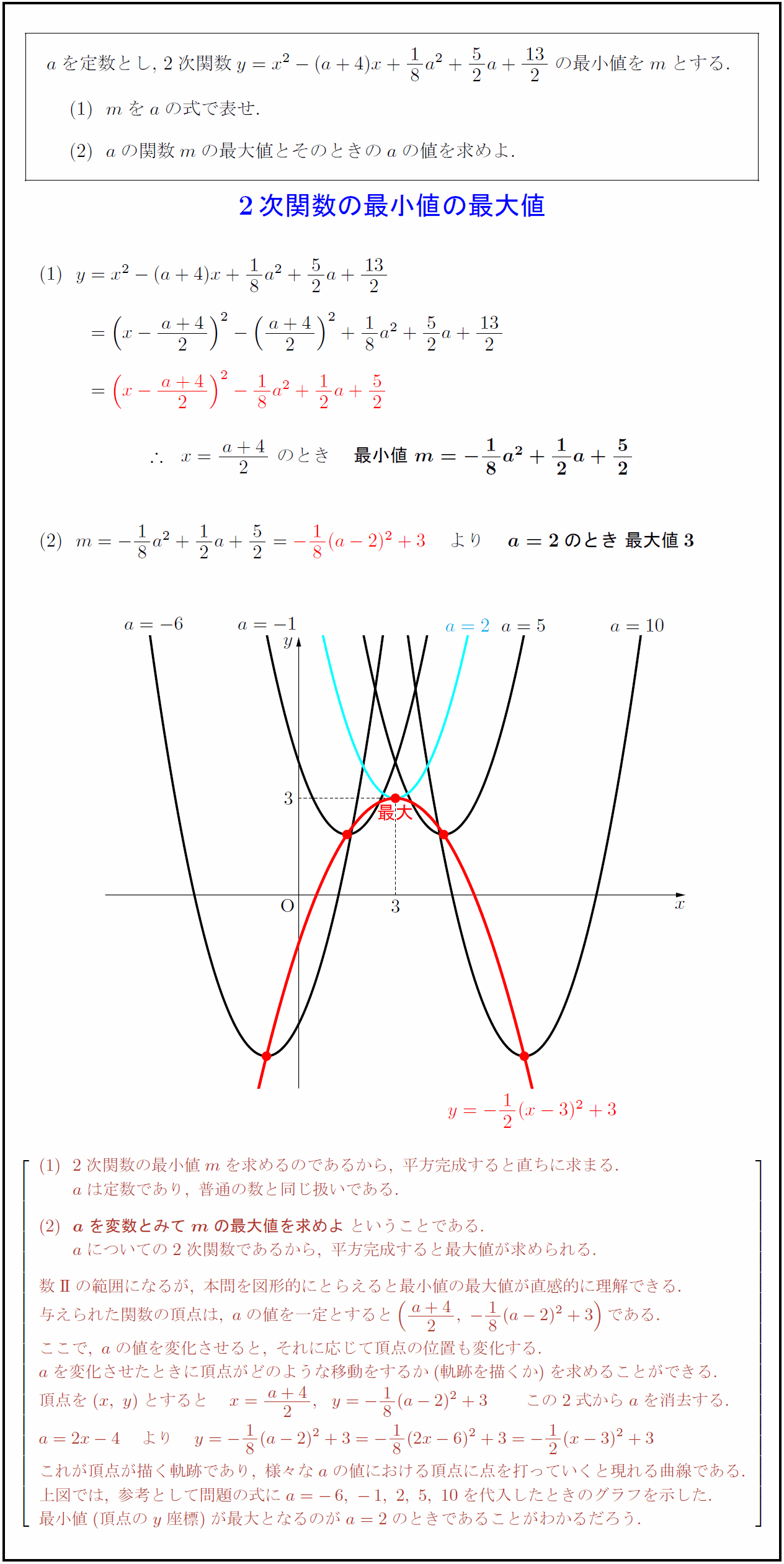
高校数学 文字を含む2次関数の最小値の最大値 受験の月

高校数学 ２次関数 教科書 問題 解答 公式 解説 学校よりわかりやすいサイト

数学 二次関数グラフの書き方を初めから解説 Youtube

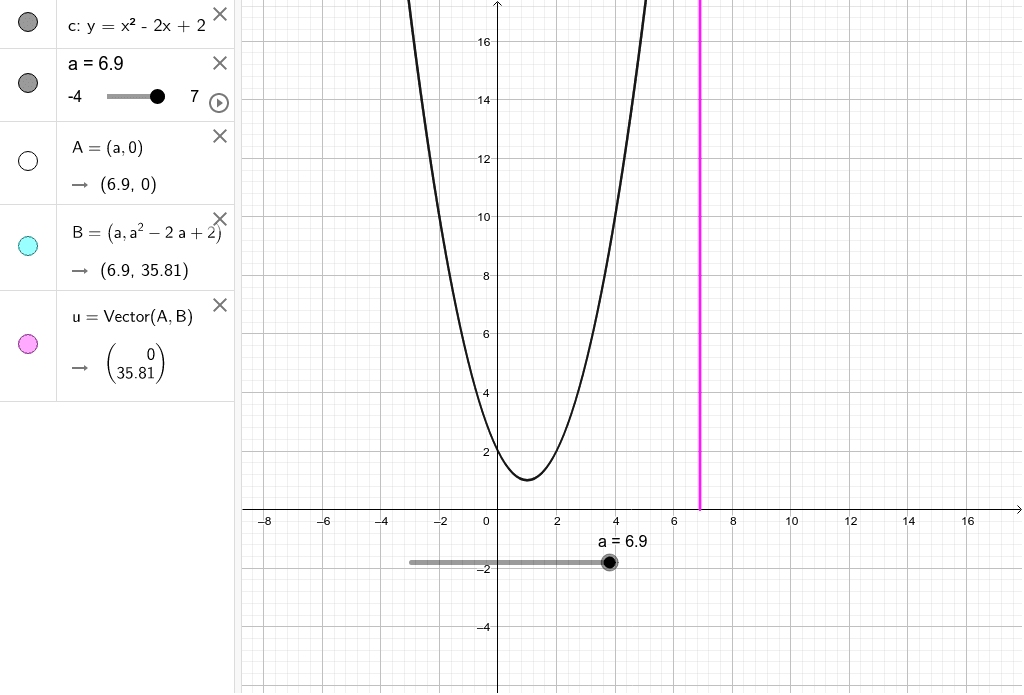
数学i 2次関数の符号 3 Geogebra

2次関数に関するチャートをまとめてアップ 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

二次関数の教え方 キムチャート 塾で高校生に数学を教える方法

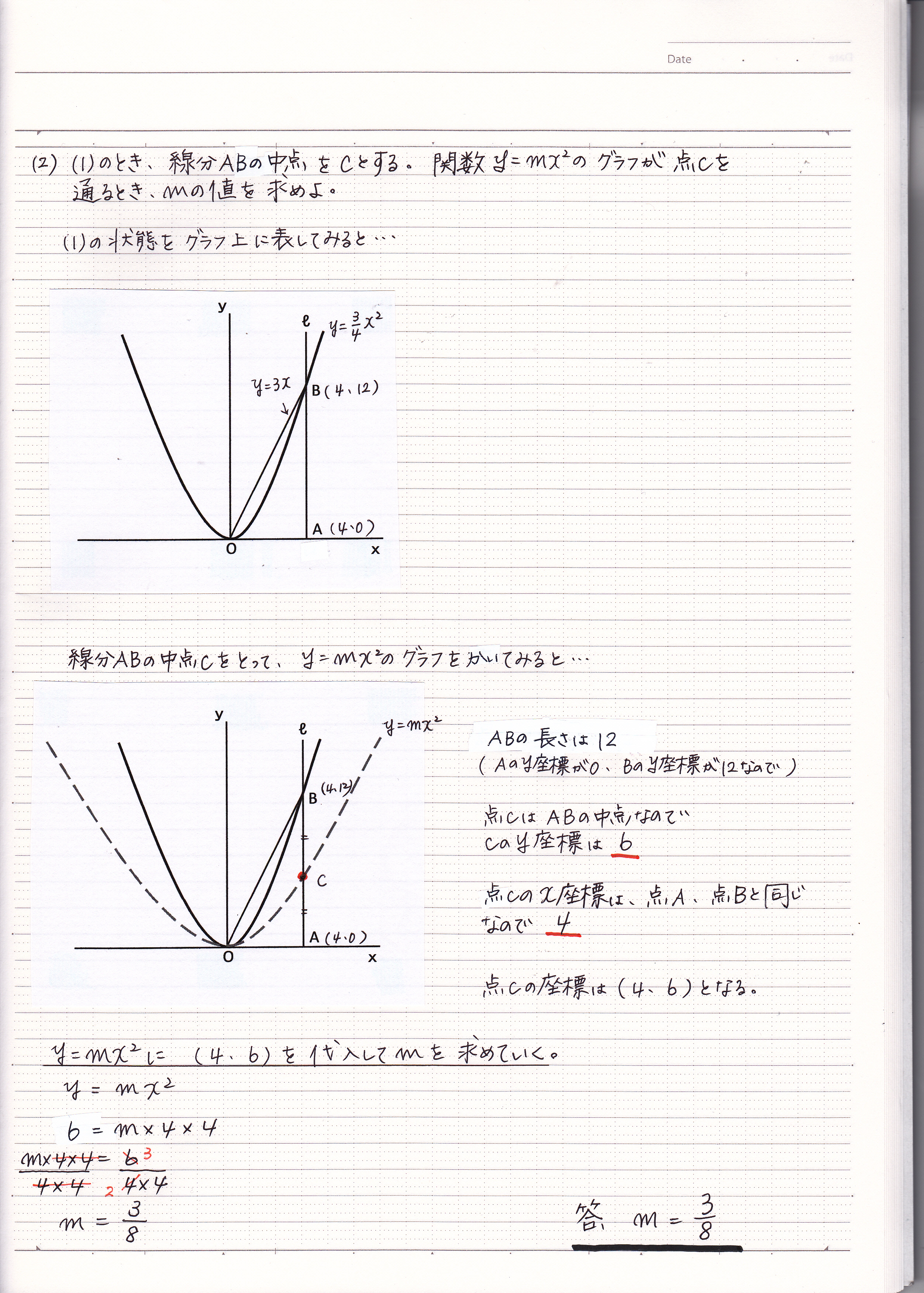
二次関数の利用の問題の解き方 グラフの問題 1 現役塾講師のわかりやすい中学数学の解き方

面白い数学の問題 二次関数 たまには本格的な数学の問題を そらの暇つぶしch

二次関数とは 公式や 最大値 最小値 決定の問題の解き方 受験辞典

２次関数y A X 2 と直線y Mx Nとの交点 中学３年生の数学 身勝手な主張

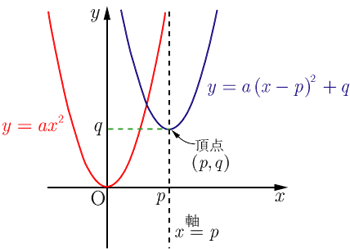
2次関数のグラフ Y A X 2 P Q

Incoming Term: 数学2次関数 最大値, 数学2次関数 場合分け, 数学2次関数 問題, 中3 数学2次関数, とある男が授業してみた 数学2次関数,