X^2 y^2 z^2=16 graph 360675
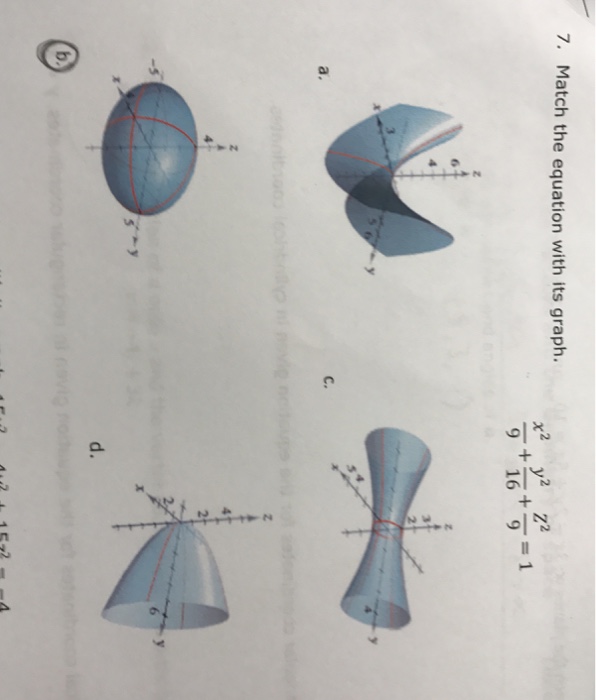
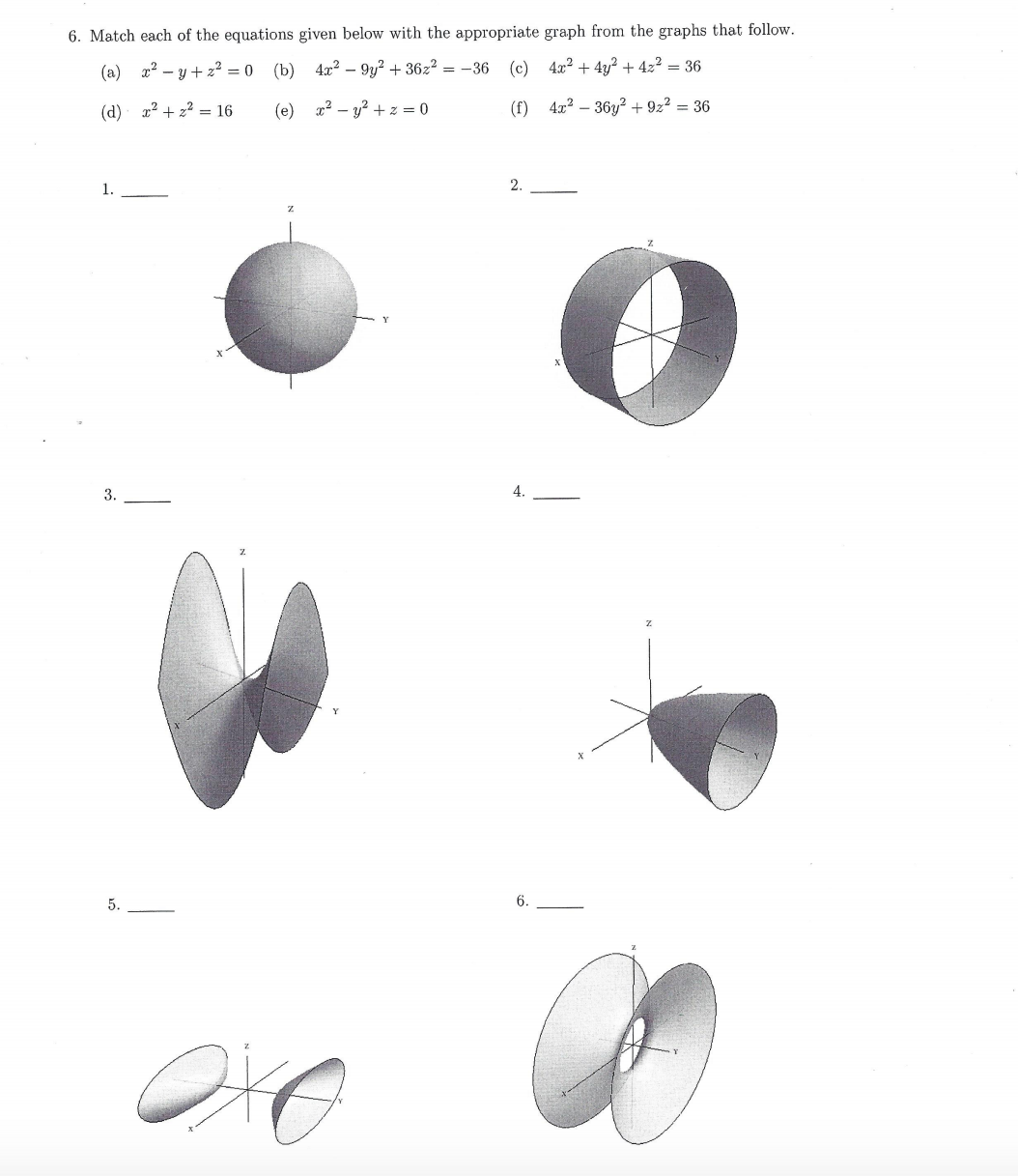
Match The Equation With Its Graph Dfrac X 2 9 Dfrac Y 2 16 Dfrac Z 2 9 1 A B C D E F Snapsolve
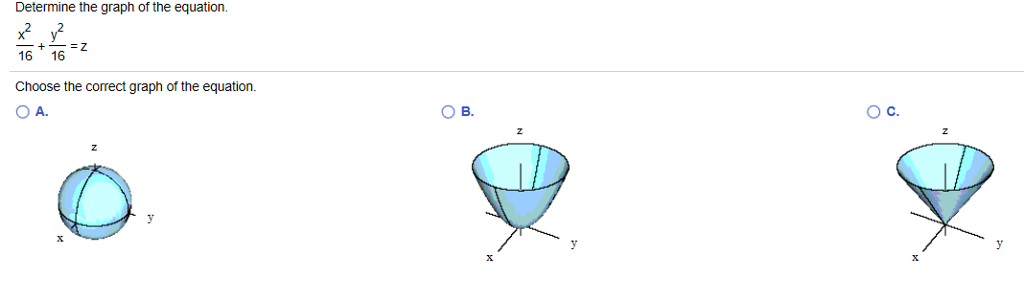
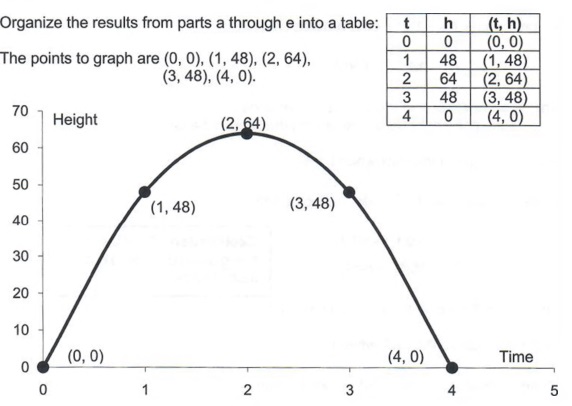
A sphere is the graph of an equation of the form x 2 y 2 z 2 = p 2 for some real number p The radius of the sphere is p (see the figure below) Ellipsoids are the graphs of equations of the form ax 2 by 2 cz 2 = p 2, where a, b, and c are all positiveCalculus Calculus questions and answers Match the equation with its graph x^2/9 y^2/16 Z^2/9 = 1
X^2 y^2 z^2=16 graph
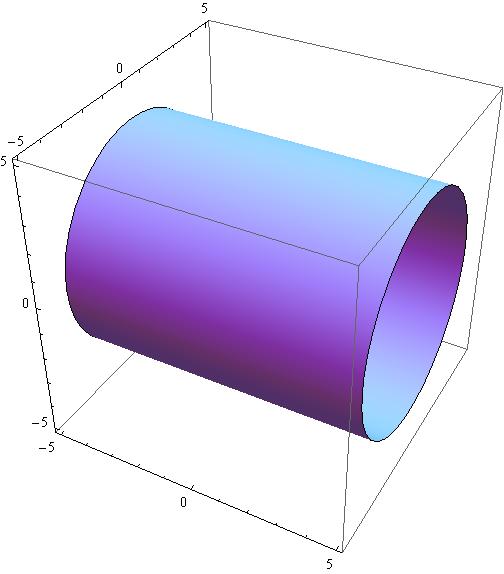
X^2 y^2 z^2=16 graph-Next, let us draw the cylinder x^2 y^2 = 2 In this cylinderUse "x" as the variable like this Examples sin(x) 2x−3;
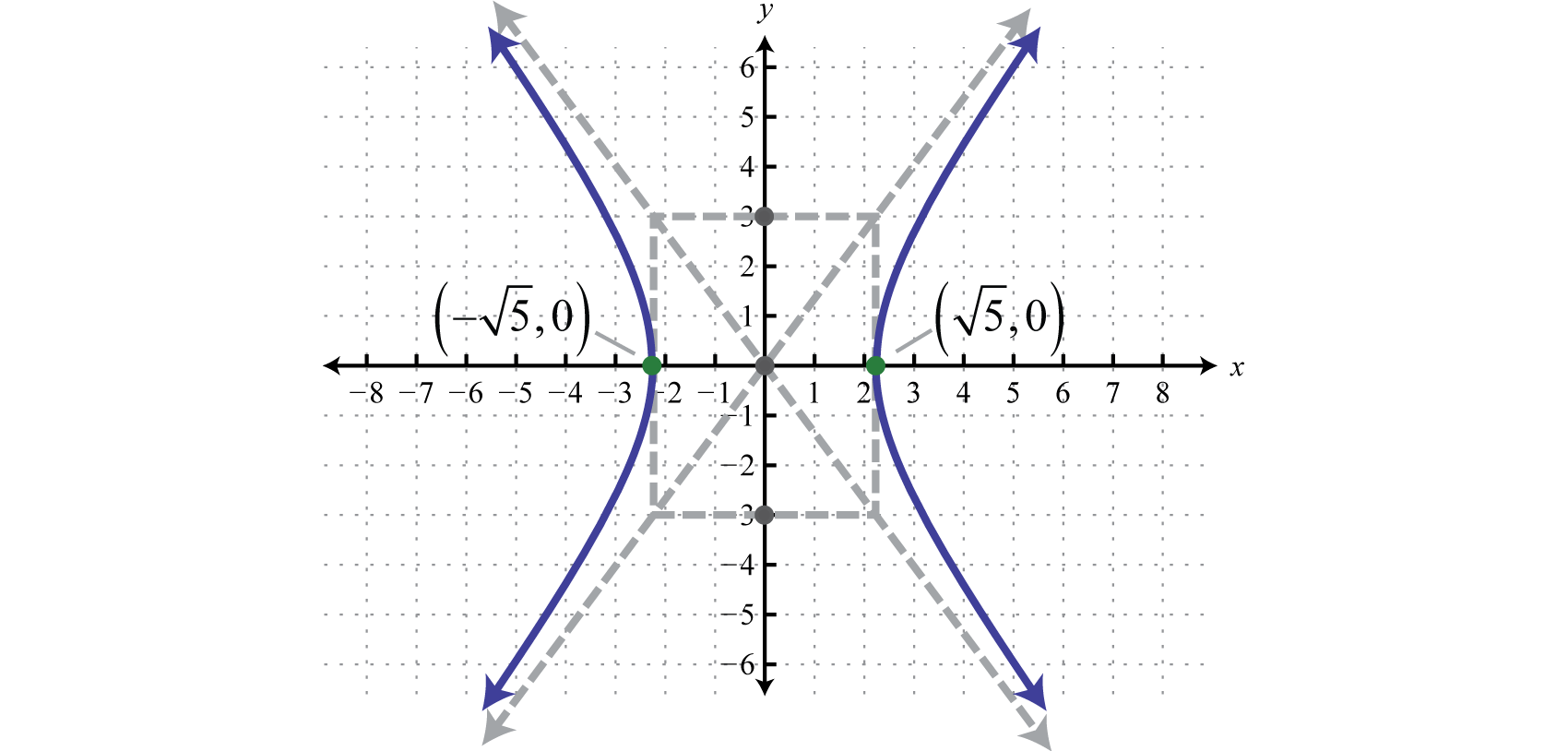
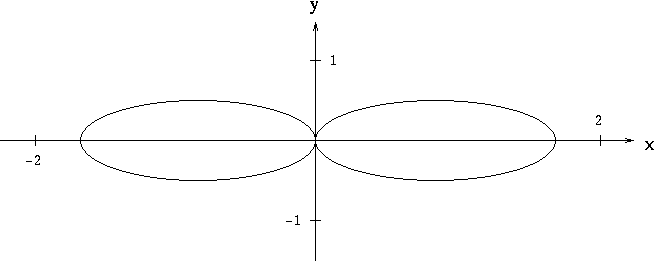
Ellipses And Hyperbolae
Answer (1 of 8) Assuming you're only working with real numbers Rearange to get that x^2y^2=0^2 This is a circle of radius 0 cenetered the orgin But if our circle is of radius 0 and at the origin, that must mean one thing the graph is just the origin SoCircleequationcalculator center (x2)^2(y3)^2=16 en Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just like running, it takesF(x,y,z) = x2 y2 y2 and the constraint is g(x,y,z) = x y z = 6 The vector equation ∇f = λ∇g gives the system 2x = λ, 2y = λ, 2z = λ Therefore, x = y = z, and as the sum is 6, then (x,y,z) = (2,2,2) and the product is 8 16
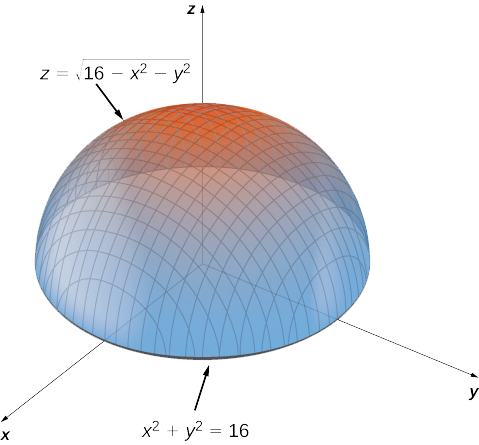
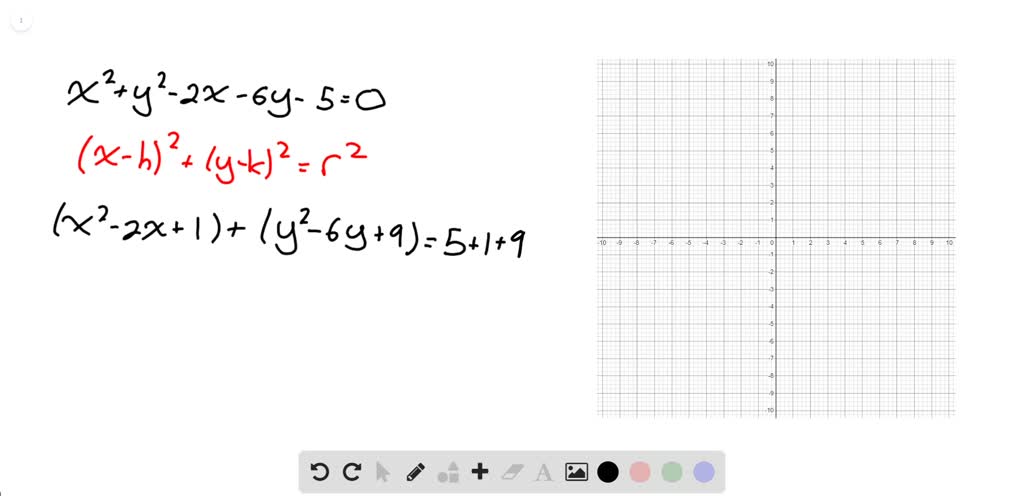
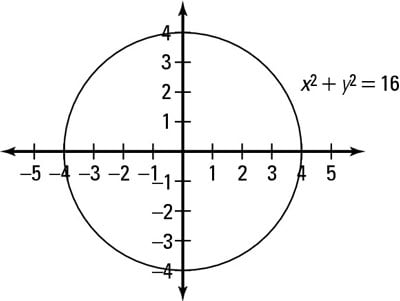
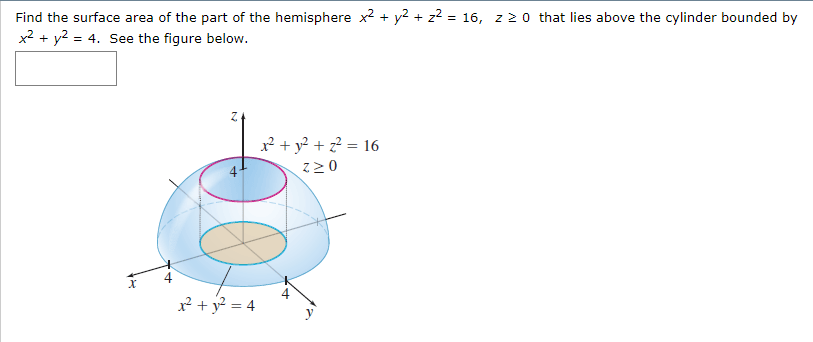
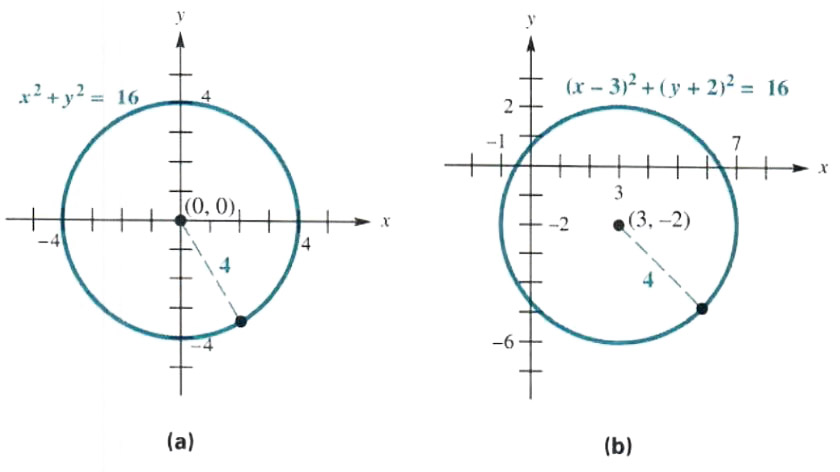
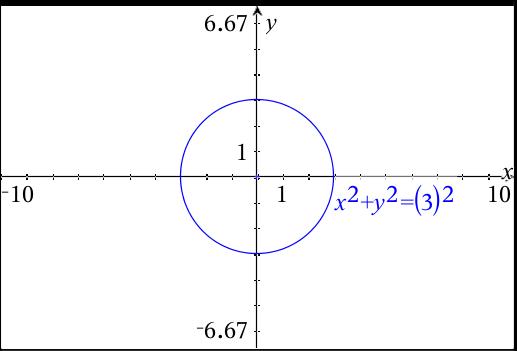
This is a circle of radius 4 centred at the origin Given x^2y^2=16 Note that we can rewrite this equation as (x0)^2(y0)^2 = 4^2 This is in the standard form (xh)^2(yk)^2 = r^2 of a circle with centre (h, k) = (0, 0) and radius r = 4 So this is a circle of radius 4 centred at the origin graph{x^2y^2 = 16 10, 10, 5, 5}Example Find the volume of the solid region above the cone z2 = 3(x2 y2) (z ≥ 0) and below the sphere x 2 y 2 z 2 = 4 Soln The sphere x 2 y 2 z 2 = 4 in spherical coordinates is ρ = 2Sin (x)cos (y)=05 2x−3y=1 cos (x^2)=y (x−3) (x3)=y^2 y=x^2 If you don't include an equals sign, it will assume you mean " =0 " It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know Note it may take a few seconds to finish, because it has to do lots of calculations
X^2 y^2 z^2=16 graphのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
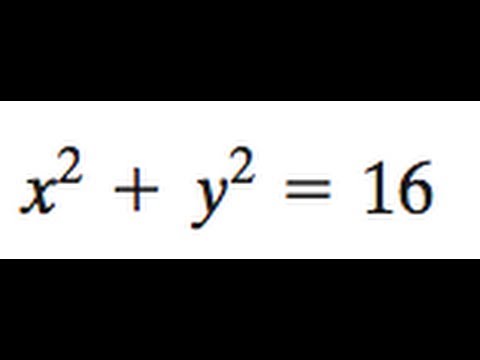 |  | |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
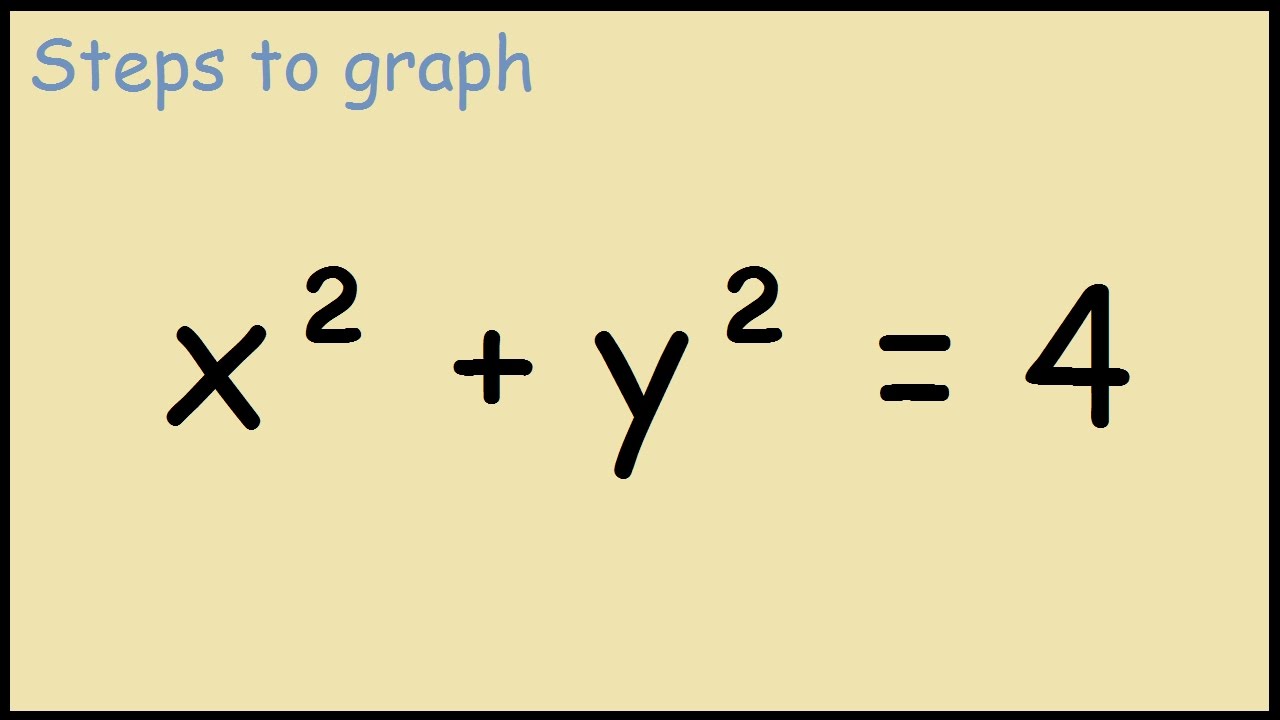 |  | |
 |  |  |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
「X^2 y^2 z^2=16 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |
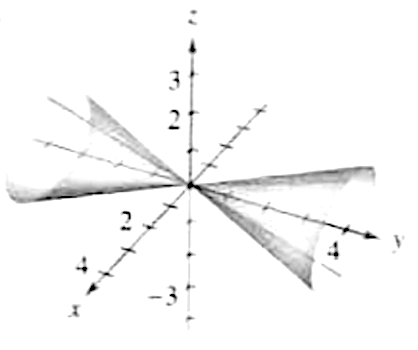
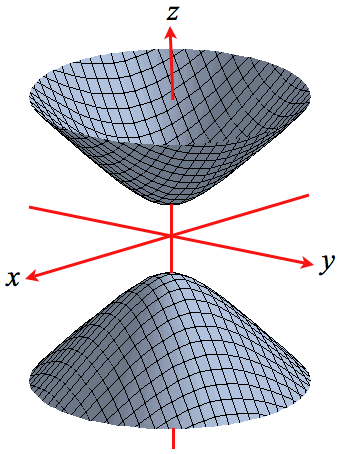
By using Pythagoras you would end up with the equation given where the 4 is in fact r^2 To obtain the plot points manipulate the equation as below Given" "x^2y^2=r^2" ">" "x^2y^2 =4 Subtract x^2 from both sides giving " "y^2=4x^2 Take the square root of both sides " "y=sqrt(4x^2) Now write it as " "y=sqrt(4x^2) '~~~~~ Calculate andShow activity on this post This figure is the (double) cone of equation x 2 = y 2 − z 2 The gray plane is the plane ( x, y) You can see that it is a cone noting that for any y = a the projection of the surface on the plane ( x, z) is a circumference of radius a with equation z 2 x 2 = a 2 Note that z = y 2 − x 2 is the semicone with z > 0, ie above the plane ( x, y) and z = − y 2 − x 2 is the semi
コメント
コメントを投稿